数学の世界には、直感に反する不思議なルールが存在します。その代表格がこれです。
$$0! = 1$$
「$0$ の階乗」が $1$ になる。
普通、$0$ を掛け算すれば答えは $0$ になりそうなものです。「$0! = 0$ の間違いじゃないの?」と思った方も多いでしょう。
学校では「これは定義(約束)だから覚えなさい」と言われることが多いですが、実はこの定義には、そうならざるを得ない強力な理由と、数学的な美しさが隠されています。
今回は、なぜ $0!$ が $1$ でなくてはならないのか、3つの視点から「深掘り」して解説します。
【高校数学教師の視点:生徒の素朴な疑問】
この単元を教えていると、必ずといっていいほど「なぜそうなるんですか?」と納得がいかない様子の生徒たちが質問に来ます。
以前の私は「これは数学上の定義(約束事)だから」と片付けてしまっていました。しかし、よく考えてみると、論理を大切にする高校生にとって「決まりだから覚えなさい」という言葉は、数学を単なる暗記科目に変え、学習意欲を削いでしまう残酷な言葉だったのかもしれません。
せっかく数学に興味を持って質問してくれた生徒たちに、数学の背後にある「美しい法則」や「必然性」をなんとかして理解してもらいたい。そんな思いで、この記事をまとめました。
1. 【パターンの発見】階段を降りていくと…
まずは一番分かりやすい、計算の規則性(パターン)から見ていきましょう。
階乗とは、$n$ から $1$ までの自然数をすべて掛ける計算です。
$$n! = n \times (n-1) \times \cdots \times 2 \times 1$$
具体的に書いてみます。
- $4! = 4 \times 3 \times 2 \times 1 = 24$
- $3! = 3 \times 2 \times 1 = 6$
- $2! = 2 \times 1 = 2$
- $1! = 1$
これらを逆順(上から下)に見てみましょう。
$4!$ から $3!$ にするにはどうすればいいでしょうか? $4$ で割ればいいですね。
同様に、$3!$ から $2!$ にするには $3$ で割り、$2!$ から $1!$ にするには $2$ で割ります。
つまり、「前の数を $n$ で割ると、次の $(n-1)!$ になる」というルールが見えてきます。
- $4! \div 4 = 3! \quad (24 \div 4 = 6)$
- $3! \div 3 = 2! \quad (6 \div 3 = 2)$
- $2! \div 2 = 1! \quad (2 \div 2 = 1)$
では、このルールを崩さずに、もう一段階降りてみましょう。$1!$ の次は $0!$ ですから、今回は $1$ で割ることになります。
- $1! \div 1 = 0!$
$1 \div 1$ は当然 $1$ です。
したがって、数の並びのルールを守るためには、$0! = 1$ でなければならないのです。もしここで $0$ にしてしまうと、美しい階段が崩れてしまいます。
2. 【場合の数】「何もしない」という1つの行動
次に、数学Aで習う「場合の数(順列)」の視点で考えてみます。
階乗は、「$n$ 個の異なるものを一列に並べる方法」の総数を表します。
- 3個(A, B, C)を並べる:ABC, ACB, BAC, BCA, CAB, CBA の 6通り ($3!$)
- 2個(A, B)を並べる:AB, BA の 2通り ($2!$)
- 1個(A)を並べる:A の 1通り ($1!$)
では、「0個のものを並べる」とはどういうことでしょうか?
これは、「並べるものが何もない」という状態です。
ここで、「0通り(並べられない)」と答えてはいけません。
「空っぽの状態がそこに1つある」と考えるのです。
例えば、空のお皿を想像してください。「お皿の上に何も乗せない」という盛り付け方は、「何もしない」という1つの方法としてカウントされます。
(プログラミングの世界でも、「何もしない処理(NOP)」は立派な1つの命令です)
「並べ方が存在しない(不可能)」のではなく、「『空集合』という並びが1つ存在する」。
だから、$0! = 1$ なのです。
【教え方のコツ:空っぽの箱の例え】
「0個を並べる」という概念がピンとこない生徒には、私はよく「空っぽの箱」の例えを使います。
箱の中に1つリンゴを入れる並べ方は1通り。では「箱の中に何も入れないという並べ方」は何通りある?と聞くと、多くの生徒は「0通り」ではなく「『何もしない』という状態が1通りある」ということに気づいてくれます。
ただ、これでも納得がいかない鋭い生徒もいます。 「先生、それなら1個を並べる時は、『1個を置く』のと『置かない』ので2通りにならないとおかしくないですか?」というツッコミです。
確かに、その視点は非常に鋭いです。なぜ1個の時は「置かない」を数えないのか? そんな「場合の数」の不思議を解消するために、次の第3章で解説する「数式の整合性」を読んでみてください。
3. 【数式の救済】コンビネーションを守れ

先ほどの生徒の疑問、「なぜ1個を並べる時は『置かない』を数えないのに、0個の時は『置かない(何もしない)』を1通りと数えるのか?」に対する答えは、実はこの第3章に隠されています。
数学において、新しいルール(定義)を決めるときに最も大切なのは、「今ある便利な公式が、どんな数字を入れても壊れないようにすること」です。
もし「1個の並べ方は2通りだ」としてしまったり、逆に「0! = 0だ」としてしまうと、これから紹介する組み合わせの公式 $_nC_k$ がすべてデタラメになってしまうのです。
$_nC_k$ 公式の崩壊を防ぐパズルのピース
高校数学で習う、組み合わせの公式を思い出してみましょう。
$$_nC_k = \frac{n!}{k!(n-k)!}$$
ここで、「3個の中から3個すべてを選ぶ」場合($_3C_3$)を考えてみます。
3個の中から3個全部取る方法は、常識的に考えて 1通り しかありません。
これを公式に当てはめて計算してみると……
$$\begin{split} _3C_3 &= \frac{3!}{3!(3-3)!} \\ &= \frac{3!}{3! \times 0!} \end{split}$$
分母に 0! が現れました。ここで計算を止めて考えてみてください。
- もし 0! = 0 だったら?分母が 0 になってしまいます(ゼロ除算)。数学では分母が 0 になることは許されず、式そのものが崩壊してしまいます。
- もし 0! = 1 だったら?$$\frac{6}{6 \times 1} = 1$$となり、現実の 1通り という答えと完璧に一致します!
数学は「整合性」の学問である
このように、0! = 1 と決めるのは、人間が勝手に決めた自分勝手な約束ではなく、「今ある美しい数式のネットワークを壊さないための唯一の選択」なのです。
1個の並べ方で「置かない」を数えないのも、そうしないと他の全ての公式が矛盾だらけになってしまうからです。
「定義だから覚えなさい」という言葉の裏には、実は「そう決めないと、数学という美しく積み上げられた城がガラガラと崩れてしまうんだよ」という、数学者たちの切実なメッセージが込められているのです。
4.【深掘り】階乗は「点」ではなく「線」だった?(ガンマ関数)
ここまで読んで、「理屈は分かったけれど、やっぱり $0! = 1$ は人間が計算しやすいように後から決めた『こじつけ』なんじゃないか?」と感じる方もいるかもしれません。
実は、私も大学生になるまではどこかでそう思っていました。しかし、その疑念を一気に吹き飛ばす、数学の深遠な真理に出会ったのです。それが「ガンマ関数」という概念です。
孤独な点がつながる瞬間
高校数学までの階乗は、$1!, 2!, 3!, 4! \dots$ と、飛び飛びの自然数だけで定義される「点」の存在でした。しかし、数学者オイラーは、この階乗を「小数」や「分数」の世界でも計算できるように、滑らかな曲線へと拡張しました。それが以下のグラフです。
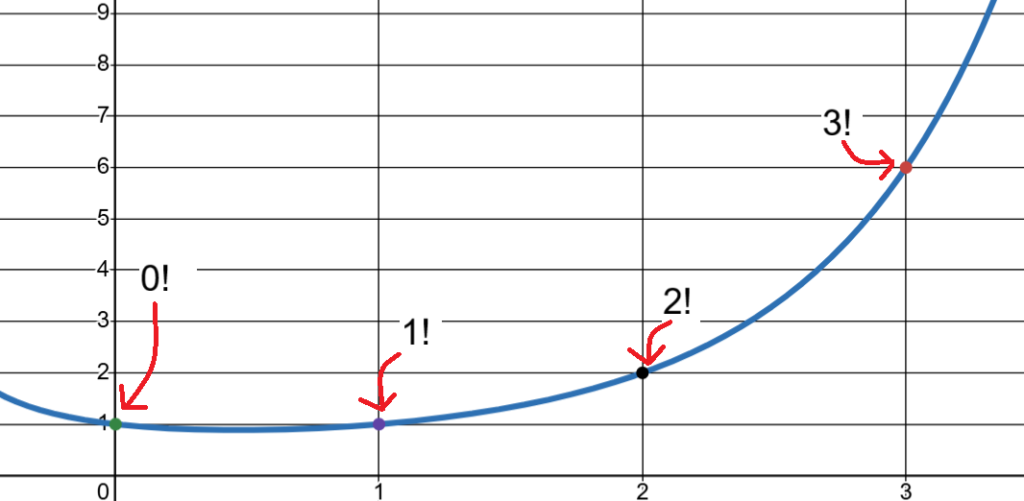
このグラフを初めて見たとき、私は全身に鳥肌が立つのを感じました。
グラフの曲線は、$1! = 1, 2! = 2, 3! = 6$ という各地点を完璧に結びながら、一つの美しいカーブを描いています。そして、そのカーブが $0!$ にあたる地点(グラフ上の $x=1$ 付近の挙動)を通過する瞬間をよく見てください。
曲線は、迷うことなくぴたりと「1」の地点を通り過ぎているのです。
ちなみに、ガンマ関数は負の数でも定義されていて
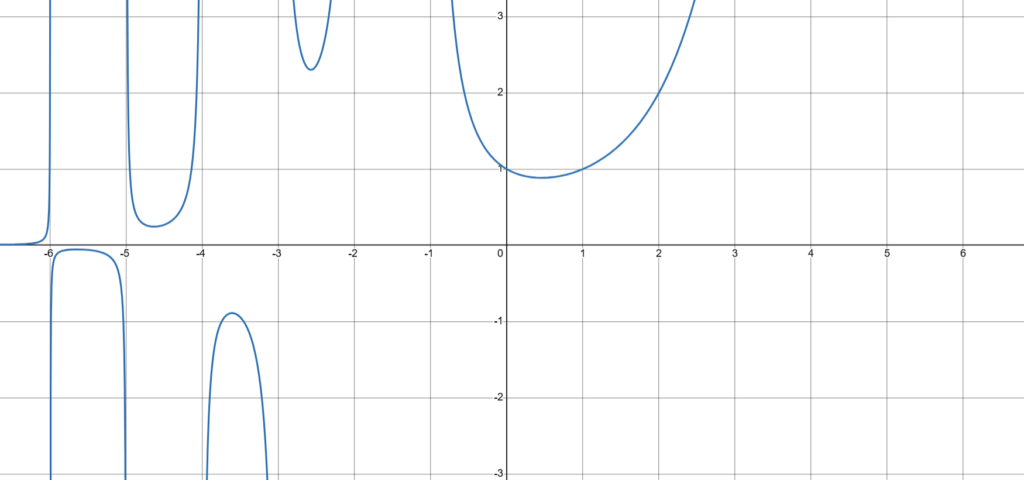
このようなグラフになる。
かなり奇妙な形をしていることが分かるのではなかろうか。
人間の約束を超えた「真理」
このグラフは、私にこう教えてくれている気がしました。
「$0! = 1$ というのは、人間が勝手に決めたルールではなく、この世界の理(ことわり)の中に、最初から組み込まれていた必然なんだ」と。
バラバラだったパズルのピースが、一枚の壮大な絵画として完成したような。あるいは、真っ暗な夜道で点々と灯っていた街灯が、一つの光の道としてつながったような。そんな感覚でした。
「定義だから覚えなさい」という一言で済ませるには、あまりにも惜しいドラマがそこにはありました。この曲線が描く「数学の意志」を知ったとき、私は数学という学問が、単なる数字のパズルではなく、宇宙の法則を解き明かすための美しい言語なのだと再確認したのです。
5.まとめ
おわりに:数学の「なぜ?」の先にあるもの
塾や学校の教室で「なぜ $0! = 1$ なの?」と聞いてくれた生徒たち。彼らの純粋な疑問は、数学の本質を突いていました。
- 「並べ方」の論理:何もしないという1つの選択
- 「数式」の整合性:公式を壊さないための唯一のピース
- 「関数」の真理:宇宙の法則が描く一本の線
こうして多角的に見ていくと、ただの暗記対象だった「定義」が、血の通った納得感へと変わるはずです。
数学は、一見すると冷たい約束事の集まりに見えるかもしれません。でも、その扉を一枚めくってみれば、そこには驚くほど美しく、一寸の狂いもない調和の世界が広がっています。
次にあなたが数学の「なぜ?」に出会ったとき、それは新しい世界の入り口かもしれません。その時はぜひ、「定義だから」と諦めずに、その先の美しさを探してみてください。



-120x68.jpg)
コメント