今回はエビングハウスの忘却曲線の考察である。対数関数までの知識があれば理解できる内容なのでぜひ読んでみてほしい。
エビングハウスの忘却曲線
エビングハウスの忘却曲線という言葉を耳にした人は多いと思う。でも，それとは何かと聞かれると正確に答えることができる人は多くなのでは思った。
エビングハウスの忘却曲線のグラフ
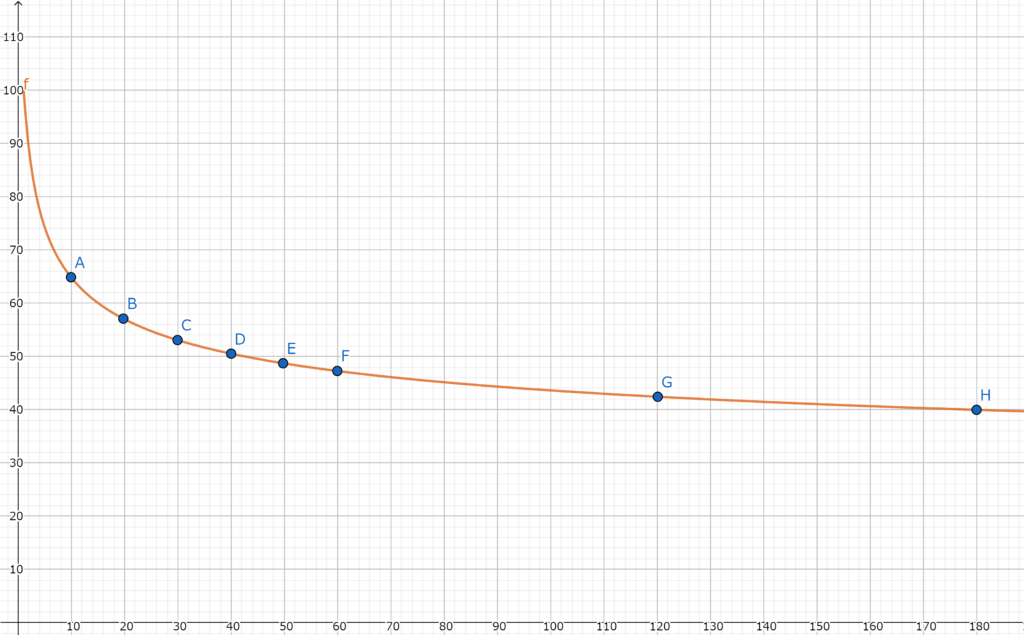
これがエビングハウスの著書に示してある忘却曲線のグラフである。式は
$$y=100\times\frac{1.84}{(\log_{10}{x})^{1.25}+1.84}$$
である。
エビングハウスの忘却曲線の本当の意味
ここで横軸が時間（分）、縦軸が記憶量（覚えている割合）と思っている方がほとんどかもしれない。しかし、本当の縦軸は節約率を表している。節約率とは一度記憶したことを、もう一度記憶するまでの時間をどれくらい節約できたかというものである。節約率の例を挙げると，初学の内容を覚えるのに10分かかったとする。そのあと，もう一度学習した際に3分で覚えることができた場合は，$10分-3分=7分$覚える時間を節約できたので，初学のときは10分かかったことから
$$\frac{7分}{10分}=0.7=70\%$$
70%の時間を節約できたという意味なのである。
よくある間違い
例えば上の図の点Hを見てほしい。180分で40％になるところである。
ここでは、100個の英単語を覚えたら180分後に40個ほどしか覚えていない。
正しくは、覚えた時間に対して40％の時間節約ができるという意味なのである。
考察１ 「時間が経過すると節約率（縦軸の値）はどうなっていくのか？」
さて、今回はこのグラフの式について考察をする。グラフを見ると分かるように、最初の60分間で急激に節約率が下がることが分かるだろう。しかし、180分以降ではその下がり幅もどんどん緩やかになっていく。ではなぜ緩やかになるのか。グラフの式からそれは分かる。
忘却曲線の方程式の右辺に変数は$\log_{10}{x}$の１つのみである。その対数が$x$を大きくしていくとどのように振舞うのかが分かればおのずと理由が分かるであろう。
$y=\log_{10}{x}$のグラフは増加関数であるが、その上がり方はどんどん緩やかになる。つまり$x$が大きなっても$\log_{10}{x}$はたいして変化がないのだ。そのことから，節約率の減少幅も時間経過していてもどんどん緩やかになるのである。
では次の問題はどうであろう。
考察２ 「最終的に節約率はどうなるのか？」
問題 経過時間を大きくしていくと節約率の値はどうなるか。
さきほど、節約率はどんどん緩やかになることは述べた。しかし、節約率はやがてどうなるのかまではまだ考えていない。なので次ではこの考察をしてみよう。
これも忘却曲線の方程式の右辺の$\log_{10}{x}$が$x$が大きくなるとどのような振る舞いをするかを考えると良い。先ほどの$y=\log_{10}{x}$のグラフは増加関数であるが、その上がり方はどんどん緩やかになることを述べたが、対数関数の特徴である「増加は緩やかになるが、ある一定の値に収束せず発散する」ということを用いる。なので$x$を大きくすると$\log_{10}{x}$は発散してしまうのだ。したがって，
$$\begin{split}\lim_{x\to\infty}({100\times\frac{1.84}{(\log_{10}{x})^{1.25}+1.84}})
&=100\times\frac{1.84}{(\lim_{x\to\infty}({\log_{10}{x}}))^{1.25}+1.84}\\
&=100\times\frac{1.84}{\infty^{1.25}+1.84}\\
&=0\end{split}$$
よって、復習等をせずにいると節約率が0％になってしまい、覚えるのに初学時と同じ時間を要してしまうのである。
まとめ
今回は高校生でも理解できるような簡単な考察をしてみた。本来の人間の記憶はどのような構造で覚えるのかという点について筆者はほぼ無知なので、完全忘却の場合などの脳に関することは脳の専門家に譲る。興味のある人はそちらの研究や探究をすすめていくと良いと思う。グラフから分かるためには、複雑に絡み合った初等関数（三角関数・指数関数・対数関数など）を理解するということが重要であることが上の方程式から分かると思う。数学の基礎というのは世の中の複雑な事柄を単純化させたときに重要であることがわかるのである。
コメント