数学IIで指数関数や対数関数を学んでいるとき、最後の計算で2次不等式が出てきて手が止まってしまう……。日々教壇に立っていると、そんな生徒を本当によく見かけます。
実は、数学IIの面白い部分を心から楽しむためには、数学Iの「2次不等式」を息をするように解ける力が必要不可欠なのです。
今回は、公式の丸暗記ではなく、グラフを書いて目で見て解く、最も確実で納得できる2次不等式の解き方を解説します。基本から、少し厄介なパターンまで網羅しました。
グラフを書けば、不等号の向きは怖くない
2次不等式を解くための最強の武器、それは「ざっくりとした2次関数のグラフを書くこと」です。
式だけで処理しようとすると、不等号の向きを間違えたり、解の範囲がこんらがってしまいます。以下の3つのステップを踏むだけで、どんな2次不等式も視覚的に解くことができます。
ステップ1:まずは「=0」の方程式として解く(x軸との交点を求める)
ステップ2:下に凸(Uの字)の放物線をざっくり書く

上の画像くらいざっくりで構いません!3種類がありますけど、問題を解くときに使うのはそのうち1つです。どれを使うのかを判断していけばよいのです。
ステップ3:不等号の向きを見て、x軸より「上」か「下」かを塗りつぶす
さっそく、具体的な例題で確認していきましょう。
例題1:基本の因数分解パターン
例題
$$x^2 – 5x + 6 > 0$$
を解け。
解説
ステップ1:方程式として解く
まずは、不等号を一旦忘れて「=0」の方程式として解き、グラフがx軸と交わる点を求めます。
$$x^2 – 5x + 6 = 0$$
$$(x – 2)(x – 3) = 0$$
$$x = 2, 3$$
ステップ2:グラフを書く
x軸に 2 と 3 の目盛りを打ち、下から突き抜けるようなUの字のグラフ(放物線)を書きます。
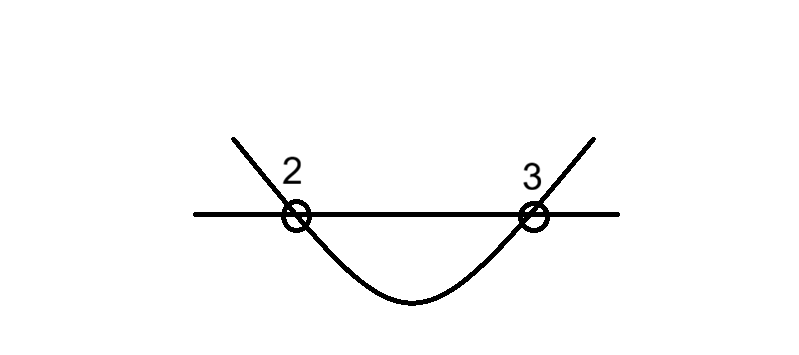
ステップ3:不等号の向きを確認する
元の式は >0 なので、グラフがx軸よりも「上側」にある部分を探せ、という指令です。
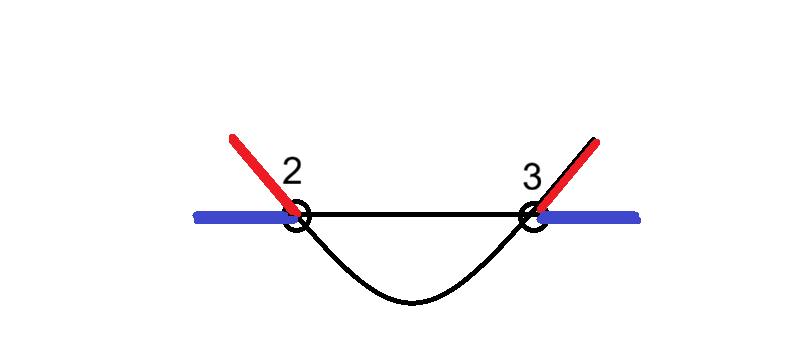
グラフを見ると、xが2より小さい範囲、あるいは3より大きい範囲で、放物線がx軸の上に飛び出していることが分かります。したがって、解は以下のようになります。
$$x < 2, 3 < x$$
例題2:解の公式を使うパターン
例題
$$x^2 – 4x + 1 \leqq 0$$
を解け。
解説
ステップ1:方程式として解く
因数分解ができないので、解の公式を使います。
$$x^2 – 4x + 1 = 0$$
$$x = \displaystyle \frac{-(-4) \pm \sqrt{(-4)^2 – 4 \times 1 \times 1}}{2 \times 1}$$
$$x = \displaystyle \frac{4 \pm \sqrt{12}}{2}$$
$$x = 2 \pm \sqrt{3}$$
交点の数字が少し複雑なルートの形になりましたが、やることは全く同じです。
ステップ2:グラフを書く
x軸の左側に 2 – √3、右側に 2 + √3 の目盛りを打ち、Uの字のグラフを書きます。
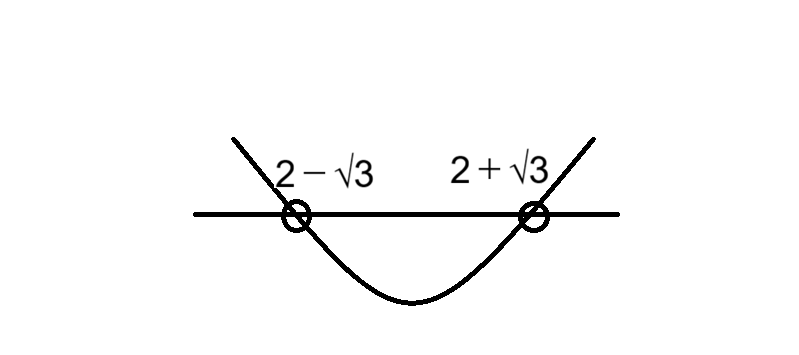
ステップ3:不等号の向きを確認する
元の式は ≦0 なので、グラフがx軸よりも「下側(またはx軸上)」にある部分を探します。
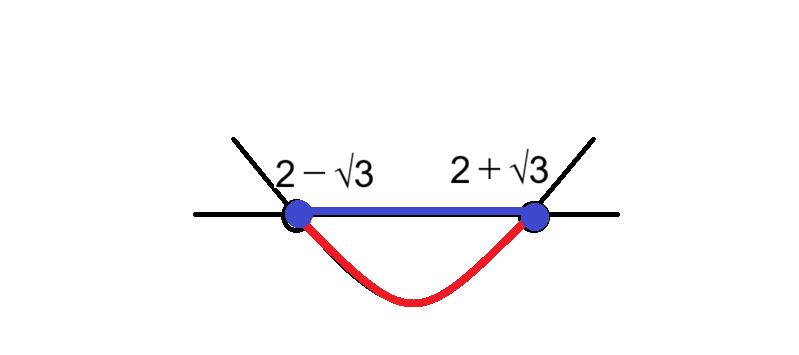
グラフを見ると、2 – √3 から 2 + √3 の間の範囲で、放物線がx軸の下に潜り込んでいることが一目で分かります。
$$2 – \sqrt{3} \leqq x \leqq 2 + \sqrt{3}$$
例題3:グラフが浮く(判別式がマイナス)パターン
最後は、生徒が最もパニックになりやすいパターンです。
例題
$$x^2 – 2x + 3 > 0$$
を解け。
解説
ステップ1:方程式として解く
解の公式を使おうとすると、ルートの中身(判別式 D)がマイナスになってしまいます。
$$D = (-2)^2 – 4 \times 1 \times 3 = -8$$
ルートの中身がマイナスになるということは、実数の範囲で「方程式の解がない」つまり「x軸と交わらない」ということを意味します。
ステップ2:グラフを書く
x軸と交わらない下に凸のグラフはどうなるかというと、x軸よりも完全に上に「プカプカと浮いた状態」になります。
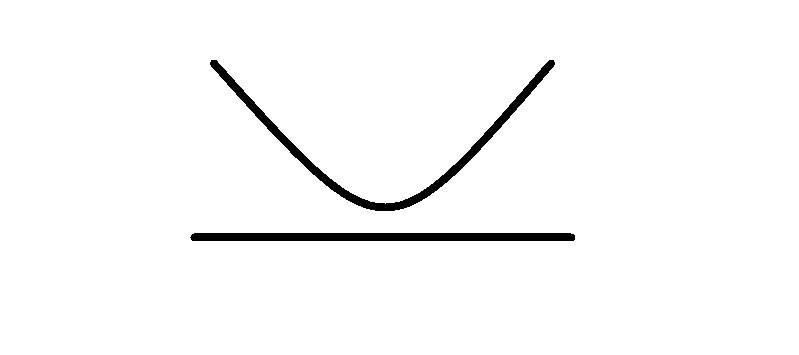
ステップ3:不等号の向きを確認する
元の式は >0 です。これは「グラフがx軸より上にあるのは、xがどんな値のときですか?」と聞いています。
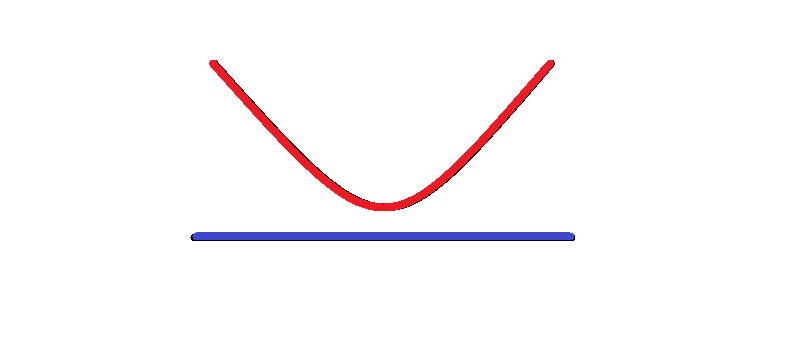
浮いているグラフを見てください。どこをとっても、すべてx軸より上にありますよね。したがって解はこうなります。
すべての実数
※補足:もし問題が
$$x^2 – 2x + 3 < 0$$
だった場合、「x軸より下にあるのはどこですか?」と聞かれていることになります。グラフは全部上にあるため、下にある部分はどこにもありません。その場合の解は「解なし」となります。
現役数学教師からのメッセージ:なぜこれを学ぶのか?
なぜ、これほどまでに2次不等式のグラフ解法を強調するのでしょうか。
それは、数学IIや数学Bなど上の学年に進んだときに、この知識が「計算のただの道具」として当たり前のように登場するからです。
たとえば、数学IIで次のような対数の問題を解くとします。
$$\log_2 x + \log_2 (x – 2) < 3$$
この式を変形していくと、最終的には今回のような2次不等式を解くことになります。ここでグラフを書く手が止まってしまうと、「対数の性質は分かっているのに、最後の計算でバツになる」という非常に悔しい思いをすることになります。
丸暗記した公式やパターンの暗記はテストが終われば忘れてしまいますが、グラフという視覚的なイメージは頭に残り続けます。次に2次不等式に出会ったら、まずは余白にサッとグラフを書いてみてくださいね。

.jpg)

コメント