1.ゼノン(Zenon)のパラドクスの「アキレスと亀」
あなたは信じられますか?
紀元前5世紀、古代ギリシャの哲学者ゼノンは、私たちの日常の常識を根底から揺さぶる、こんなパラドックス(矛盾)を提唱しました。
俊足の英雄アキレスは、先にスタートしたノロマな亀に、永遠に追いつくことができない。
もちろん、現実ではアキレスは亀に簡単に追いつけます。しかし、ゼノンの論理はあまりに完璧でした。
1-1.🐢 なぜアキレスは追いつけない? ゼノンの主張
ゼノンは言います。アキレスが亀に追いつくためには、まず「亀がいた場所」に到達しなければならない。しかし、アキレスがその地点に着くまでに、亀は少しだけ前に進んでしまう。

この「追いつく→少し進まれる」という過程は、永遠に無限に繰り返されるため、アキレスは無限のステップをこなさなければならず、結果として永遠に亀に追いつけない—これがゼノンの主張です。
1-2.視覚的に見てみると👀
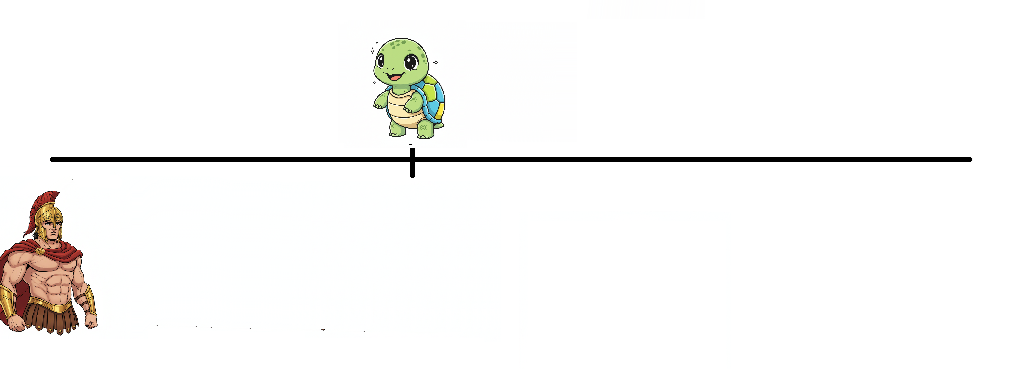
スタート段階では亀は前を走っている(歩いている)
亀のスタート地点に印をつけてそこまでアキレスが走る
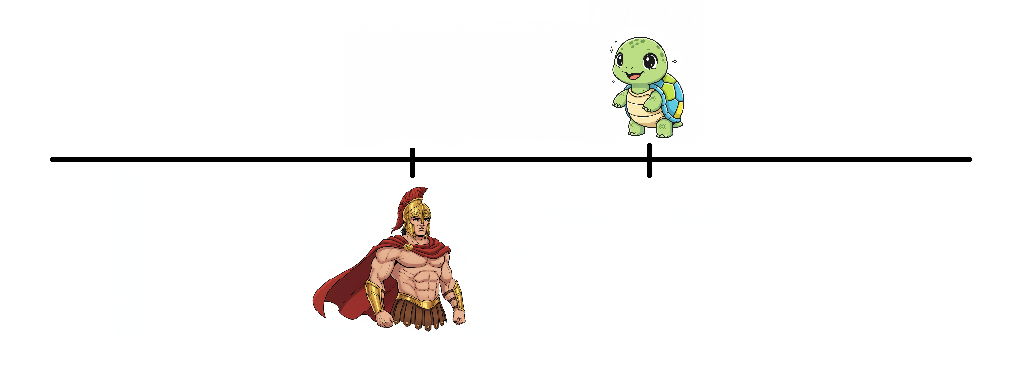
アキレスが亀のスタート地点まで来ました。
その時間で亀は若干進むのでその地点に印をつけます。
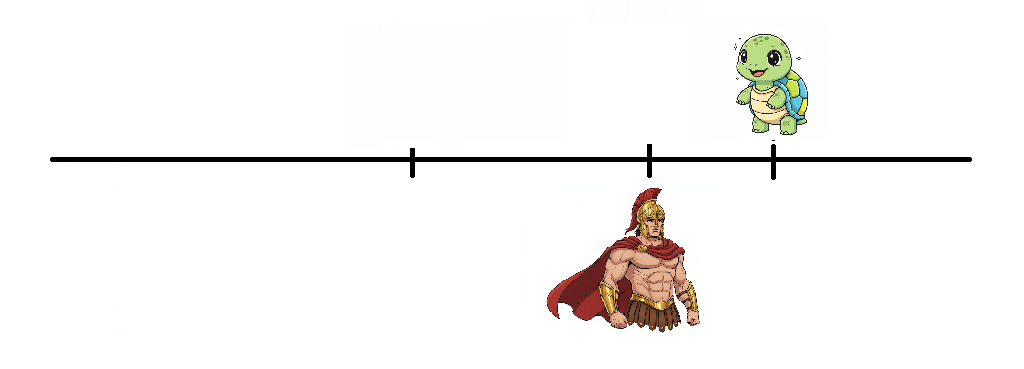
アキレスが先ほど印をつけた地点まで来ました。
その時間で亀は若干進むのでその地点に印をつけます。
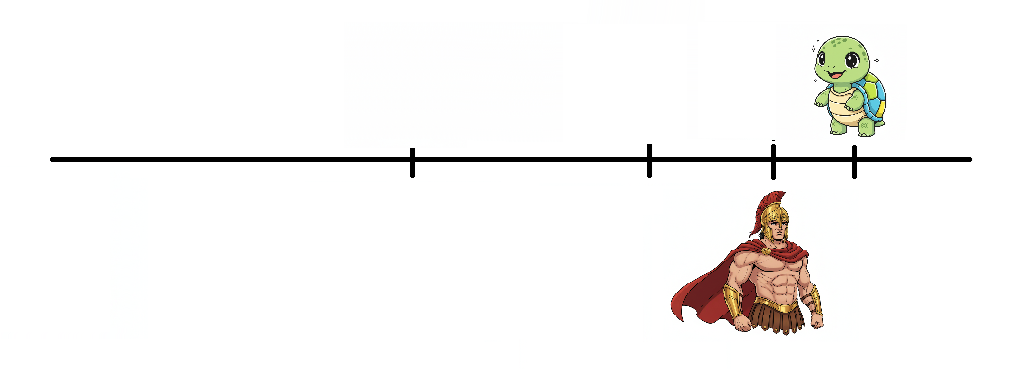
アキレスが先ほど印をつけた地点まで来ました。
その時間で亀は若干進むのでその地点に印をつけます。
以下無限に繰り返す。。。
アキレスはいつまでも亀に追いつくことができない。
1-3.💡 数学の出番だ!「無限」の謎を解く鍵
古代の人々はこのパラドックスに頭を悩ませましたが、この論理的な矛盾を打ち破る鍵は、実はあなたが高校で学ぶ「解析学(極限)」の考え方にあります。
無限に続く足し算、つまり無限級数。これこそが、アキレスの運命を決定づける数学の魔法です。
さあ、この古代からの難問を、あなたの数学の知識で打ち破りましょう。 無限のステップが、なぜ有限の時間で終わるのか?その驚くべき答えを、この先で解き明かします。
2.無限を操る魔法! 解析学の切り札「無限等比級数」
無限等比級数とは等比数列を無限に足しあげたものです。
2-1.🐢 哲学的な難問:アキレスと亀のパラドクスの概略

古代からの疑問:無限のプロセスは終わるのか?
私たちがこれから挑むのは、紀元前5世紀にゼノンという哲学者が提唱した、最も有名で人を惑わす論理パズルの一つ、「アキレスと亀」のパラドックスです。
物語は単純です。俊足の英雄アキレスが、ノロマな亀にハンデを与えて競争を始めます。現実では、アキレスが勝つのは当たり前。しかし、ゼノンは論理だけでこの常識を打ち破ろうとしました。
2-2.論理の罠:「無限のステップ」の連鎖
ゼノンが指摘したのは、「追いつくまでの過程」の奇妙さです。
- アキレスがスタート地点から、亀がいた最初の地点 $P_0$ に着く。
- その間に亀はわずかに進み、新しい地点 $P_1$ にいる。
- アキレスが $P_1$ に着く。その間に亀はさらにわずかに進み、新しい地点 $P_2$ にいる。
- この「追いつく→わずかに進まれる」というステップは、どんなに細かく区切っても、理論上、無限に続く。
ゼノンの主張の核心はこれです。
アキレスが亀に追いつくためには、無限に続くこれらのステップをすべてクリアしなければならない。
無限の数のステップをこなすには、無限の時間がかかるのではないか?
つまり、ゼノンの論理に従うと、アキレスは永遠に亀に追いつくことができないはずなのです。
3.💡 なぜ、私たちは「追いつける」ことを知っているのか?
私たちはこの論理に直面しても、「そんなバカな。追いつけるに決まっている!」と感じます。しかし、その直感を論理的に説明するのは簡単ではありません。
なぜなら、このパラドックスの正体は、私たちが合計時間を表すときに生まれた無限の足し算(無限級数)にあるからです。
$$T = t_1 + t_2 + t_3 + t_4 + \cdots$$
無限個の数を足し合わせているのに、なぜ答えが有限の値(決まった時間)になるのか?
これが、古代の哲学者たちを悩ませた「無限」の最大の謎です。この哲学的な難問に、高校で学ぶ解析学(極限)の知識が、「無限のプロセスでも有限の結果が得られる仕組み」という明確な答えをもたらします。その鍵こそが、次で解説する無限等比級数なのです。
3-1.ステップ1:アキレスの「足し算のルール」を見破る
アキレスがそれぞれの区間を進むのにかかった時間を具体的に見てみましょう。
(アキレス:$10\text{m/s}$、亀:$1\text{m/s}$、ハンデ:$100\text{m}$)
- $t_1$:$100\text{m}$を進む時間 $\rightarrow 10\text{秒}$
- $t_2$:次の $10\text{m}$を進む時間 $\rightarrow 1\text{秒}$
- $t_3$:次の $1\text{m}$を進む時間 $\rightarrow 0.1\text{秒}$…

この時間の並び $10, 1, 0.1, 0.01, \cdots$ は、前の項に常に一定の数、この場合は $0.1$ をかけると次の項が得られます。このような数列の和を、数学では無限等比級数と呼びます。
アキレスの級数は、初項 $a=10$、公比 $r=0.1$ の等比級数であることがわかりました。
3-2.ステップ2:無限の和が有限になるための条件
どんな無限級数でも答えが有限になるわけではありません。たとえば、$1 + 2 + 3 + 4 + \cdots$ は無限大に発散してしまいます。
しかし、無限等比級数が有限の値に収束(答えが出る)するためには、たった一つのシンプルな条件があります。
【収束の条件】
$$\text{公比 } r \text{ の絶対値が } 1 \text{ より小さい}: \quad |r| < 1$$
これは、公比 $|r|$ が $1$ 未満、つまり $r$ が $0.1$ や $0.5$ のような数であれば、項が進むにつれて足していく数が $0$ に猛烈なスピードで近づいていくからです。無限に足しても、合計は有限の値に収束します。
アキレスの級数では公比 $r = 0.1$ であり、もちろん $|0.1| < 1$ を満たしています。これで、アキレスが追いつけるという数学的な確証が得られました!
3-3.ステップ3:解析学の切り札!魔法の公式を使いこなす
公比 $|r|<1$ の場合、無限等比級数 $S$ を求めるための公式があります。このシンプルな公式こそが、無限の足し算を一瞬で有限の値に変換する、解析学の核心です。
【無限等比級数の和の公式】初項を$a$ , 公比を$r$とするとその無限等比級数$S$とすると
$$S = \frac{a}{ 1 – r }$$
で表すことができる。
4.ついに決着! パラドックスの完全な解明 🎯
この公式を、アキレスが亀に追いつく合計時間 $T$ の計算に適用します。
- 初項 $a = 10$
- 公比 $r = 0.1 = \frac{1}{10}$
$$T = \frac{a}{1 – r} = \frac{10}{1 – 0.1} = \frac{10}{0.9}$$
$$T = \frac{10}{\frac{9}{10}} = 10 \times \frac{10}{9} = \frac{100}{9} \approx 11.111\dots\text{秒}$$
結論:
ゼノンが主張した無限のステップ(無限級数)は、解析学の極限の概念によって、たったの $\frac{100}{9}$ 秒という有限の時間に収束することが証明されました。古代からの難問は、高校で学ぶ「数列」と「極限」の知識によって、見事に論破されたのです。
5.結び:身近なところにも潜む無限の美しさ

無限級数の考え方は、ゼノンのパラドックスを解決するだけでなく、微積分をはじめとする現代科学のあらゆる基礎を支えています。たとえば、$0.999\cdots = 1$ の証明も、この無限等比級数を使うとシンプルに説明できます。
無限を扱う解析学は、世界を論理的に解明するための強力なツールです。無限を「操る」ことができるのが、数学の醍醐味なのです。




コメント