数学Ⅰでの三角比,数学Ⅱでの三角関数において次のような公式を見たことある人はほとんどかと思います。これらの公式をみなさんはどのように覚えましたか?丸暗記している人もいたかと思います。今回はこれらの公式を簡単な2つのことを意識するだけで変換できてしまう方法を紹介したいと思います。
前提知識
この変換公式を考えるうえで前提となる知識があるのでそのことをここで述べておく。それは$\theta$の角度に対して($\theta$が第何象限かが分かれば),$\sin\theta$,$\cos\theta$,$\tan\theta$が正の数か負の数かが分かっているかである。例えば,$\theta$が第2象限の角のとき,$\cos\theta$は負の数である。といった感じである。もし,ここで正負の値が怪しい人は次の項も見ていってほしい。完璧だという人は,変換公式の考え方まで飛んでも大丈夫である。
三角比の正負の値
ここで押さえておいてほしいことがある。雑な言い方なのでここでは厳密性は気にしないでほしい。押さえておいてほしいことは,$\sinはy座標$,$\cosはx座標$,$\tanは傾き$である。では実際に見ていこう。
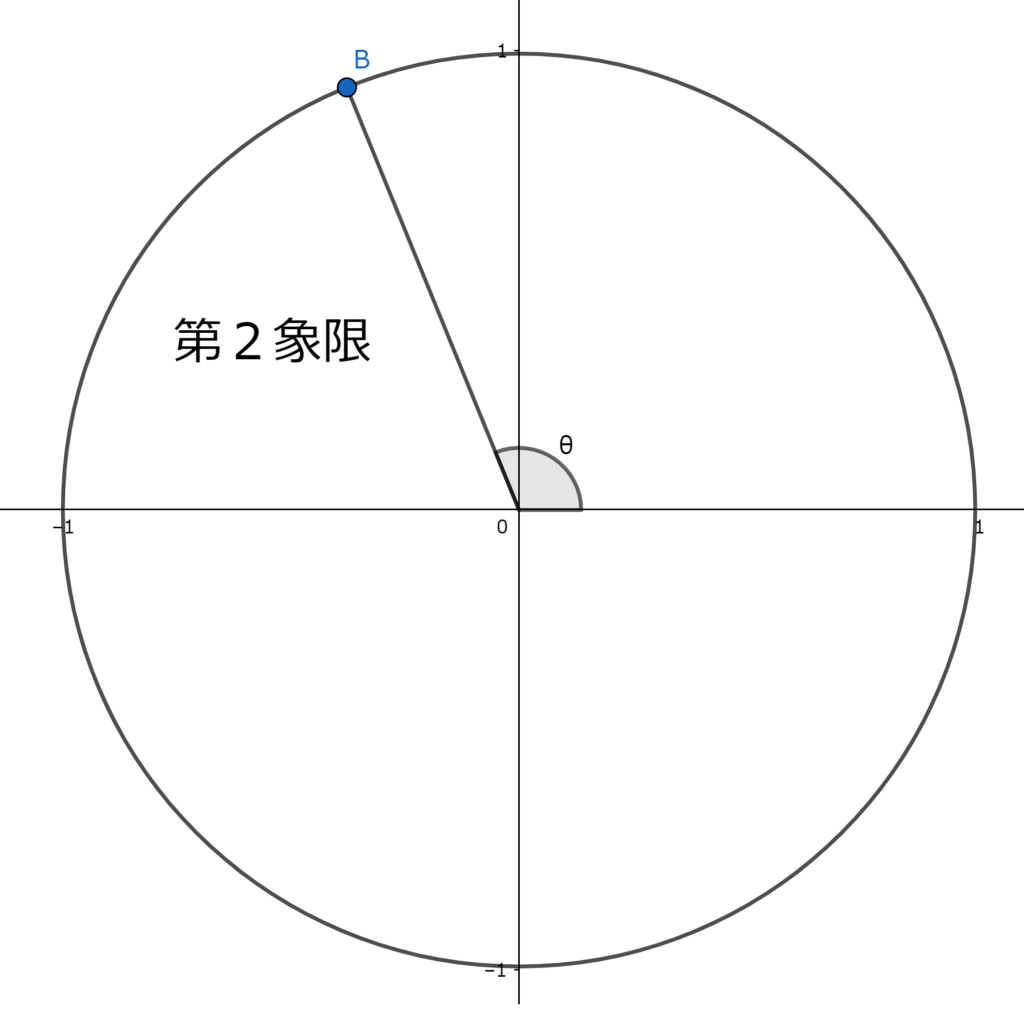
例えば,$\theta$は第2象限の角である。そこで中心から動径が$\theta$となるところに点Bをとる。この点Bの座標を見れば,$x座標$は負の数,$y座標$は正の数,傾きは負の数である。したがって,$\theta$は第2象限の角であるときは$\sin\thetaは正の数$,$\cos\thetaは負の数$,$\tan\theta$は負の数となる。これをしっかり理解して次の変換の公式にうつろう。
変換公式の覚え方
変換公式の右辺は次のような特徴があるのをご存じだろうか。
・角度の部分が$\theta$のみ
・$\sin\theta,\cos\theta,\tan\theta$ がすべて単独である。(和や積の形ではない)
このことから,三角比の変換は次の2つのことにが分かればよいのだ。
・符号
・$\sin\theta,\cos\theta,\tan\theta$ のどれを使えばよい
ではどのようにして,符号と$\sin\theta,\cos\theta,\tan\theta$のどれを使うかの判断はどこですればよいのかを解説する。
符号の判断
符号は先ほど三角比の正負の値のところと絡めて考える。例えば$\sin(90°-\theta)$の符号は$(90°-\theta)$の角が第何象限なのかを意識しよう。でも,$\theta$が分かっていないのに,$(90°-\theta)$の角が分かるわけないと思います。そうなんですが,変換の公式では$\theta$はちょっとの角と思ってください。(10°くらいの角度)そうすれば,$(90°-\theta)$は80°くらいだから第1象限になります。よって,$\sin$の第1象限は正の数だから+となるわけです。
$\sin\theta,\cos\theta,\tan\theta$ のどれを使えばよい
変換する前の角度の$\theta$以外の部分に着目します。例えば$\sin(90°-\theta)$であれば,90°の部分です。他にも,公式では180°,270°,360°なども出てきます。そこで,こんな部類分けをします。90°,270°のパターンと180°,360°のパターンの二つです。では,これらを部類分けしてどう考えるんかというと次のように覚えてください。
・90°,270° → 変える
・180°,360° → そのまま
このような感じです。
ここで変えるとは変えるとはどういうことかというと
・$\sin↔\cos$
・$\tan$↔$\frac{1}{\tan}$
よって,$\sin(90°-\theta)$の変換は変えるので$\cos$になることが分かる。

要点まとめ
結局次の2つのことに注意すれば変換できてしまう。
・角度の部分は第何象限なのか
・角度の$\theta$以外の部分は何度なのか
次はこの事実を用いて公式をいくつか導いてみよう。
公式を導こう
例題
(1) $\sin(90°+\theta)$
(2) $\cos(180°-\theta)$
(3) $\tan(180°+\theta)$
(4) $\sin(270°+\theta)$
(5) $\cos(\theta-180°)$
(6) $\tan(\theta-90°)$
解答・解説
(1) 角度を見て第何象限なのか,$\theta$以外の角度は何度かを見ると$90°+\theta$なので,第2象限であり,$\theta$以外の角度は90°となる.よって頭の中では次のように考えている.
$\sin$の第2象限は正の数だから+である.
90°だから変えるので$\sin$から$\cos$に変える.
つまり,$$\sin(90°+\theta)=\cos\theta$$
(2) 角度を見て第何象限なのか,$\theta$以外の角度は何度かを見ると$180°-\theta$なので,第2象限であり,$\theta$以外の角度は180°となる.よって頭の中では次のように考えている.
$\cos$の第2象限は負の数だから$-$である.
180°だからそのままなので$\cos$から変えない.
つまり,$$\cos(180°-\theta)=-\cos\theta$$
(3) 角度を見て第何象限なのか,$\theta$以外の角度は何度かを見ると$180°+\theta$なので,第3象限であり,$\theta$以外の角度は180°となる.よって頭の中では次のように考えている.
$\tan$の第3象限は正の数だから$+$である.
180°だからそのままなので$\tan$から変えない.
つまり,$$\tan(180°+\theta)=\tan\theta$$
(4) 角度を見て第何象限なのか,$\theta$以外の角度は何度かを見ると$270°+\theta$なので,第4象限であり,$\theta$以外の角度は270°となる.よって頭の中では次のように考えている.
$\sin$の第4象限は負の数だから$-$である.
270°だから変えるので$\sin$から$\cos$に変える.
つまり,$$\sin(270°+\theta)=-\cos\theta$$
(5) 負の角度(時計回りの方向)でも,同様に考えることができる.角度を見て第何象限なのか,$\theta$以外の角度は何度かを見ると$\theta-180°$なので,第3象限であり,$\theta$以外の角度は180°となる.よって頭の中では次のように考えている.
$\cos$の第3象限は負の数だから$-$である.
180°だからそのままなので$\cos$から変えない.
つまり,$$\cos(\theta-180°)=-\cos\theta$$
(6) 負の角度(時計回りの方向)でも,同様に考えることができる.角度を見て第何象限なのか,$\theta$以外の角度は何度かを見ると$\theta-90°$なので,第4象限であり,$\theta$以外の角度は90°となる.よって頭の中では次のように考えている.
$\tan$の第4象限は負の数だから$-$である.
90°だから変えるので$\tan$から$\frac{1}{\tan}$に変える.
つまり,$$\tan(\theta-90°)=-\frac{1}{\tan\theta}$$
実践問題(問題集レベル)
次は実践問題を出題しますので解けた方はぜひ答えをコメント欄に書き込んでみてください。
問題
(1)$$\sin^{2}(270°+\theta)+\cos^{2}(90°+\theta)$$
(2)$$\frac{1}{\tan^{2}(90°-\theta)}-\frac{1}{\cos^{2}(180°-\theta)}$$
この2問です。ぜひ解いてみてください。



コメント