学習指導要領では中学３年生のときに、初めて根号を学ぶことになっている。そして、 $\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$ の近似値は語呂合わせで暗記した人も多いと思う。しかしながら、それら以外の根号の値は覚えている人は少ないのではないか。私も先ほどの３つくらいしか覚えていない。そこで今回は $\sqrt{6}$ や $\sqrt{7}$ などの近似値の求め方の一つを紹介したいと思う。
今回は数列の漸化式の知識を使う。
ニュートン・ラフソン法
根号の近似値を求める方法いくつかある。そこで今回は求め方のひとつである「ニュートン・ラフソン法」を使って求めていくのだが、さっそくニュートン・ラフソン法を紹介する。
$p$を自然数とし，$\sqrt{p}$は無理数とする．数列$a_{n}$が次の漸化式$$a_{1}=x\hspace{10pt},\hspace{10pt}a_{n+1}=\frac{1}{2}(a_{n}+\frac{p}{a_{n}})\hspace{10pt}(aはa-1<\sqrt{q}<aを満たす自然数とする)．$$を満たすとき，数列$a_{n}$の具体的な値を求めることによって，いくらでも$\sqrt{p}$に近い有理数を求めることができる．
ニュートン・ラフソン法による漸化式の性質
先ほどの漸化式には次のような性質がある．
1 すべての自然数$n$について，$a_{n}$は有理数である．
2 すべての自然数$n$について，$\sqrt{p}<a_{n}$が成り立つ．
3 すべての自然数$n$について，$a_{n+1}<a_{n}$が成り立つ．
１から順に証明していこう。
1.の証明
自明であるといっても差し支えない気がするが証明をする。
帰納法により証明する．
[1]$n=1$のとき$x$は自然数なので$a_1$は自然数より有理数となる．
[2]$n=k$のとき成り立つ，つまり$a_k$は有理数と仮定する．
$n=k+1$のときは$$a_{k+1}=\frac{1}{2}(a_{k}+\frac{p}{a_{k}})$$より，有理数の和差積商は有理数になることと，右辺は仮定より$a_k$は有理数であり，題より$p$は自然数なので有理数となる．したがって，$a_{k+1}$も有理数となる．
[1]，[2]よりすべての自然数$n$について，$a_{n}$は有理数である．
2.の証明
帰納法により証明する．
[1]$n=1$のとき$a_1=x$なので，題より$\sqrt{p}<a$であるから$\sqrt{p}<a_1$より，成り立つ．
[2]$n=k$のとき，$\sqrt{p}<a_k$が成り立つと仮定する．
$n=k+1$のとき$a_k>0$かつ$\frac{p}{a_{k}}$$>0$なので相加相乗平均の関係より，$$\begin{split}a_{k+1}&=\frac{1}{2}(a_{k}+\frac{p}{a_{k}})\\&\geqq\sqrt{a_{k}\times\frac{p}{a_{k}}}\\&=\sqrt{p}\end{split}$$ここで仮定より，$\sqrt{p}<a_k$から$\sqrt{p}\neq a_k$なので相加相乗平均の等号が成り立つことはないので，$\sqrt{p}<a_{k+1}$より$n=k+1$のときも成り立つ．
[1]，[2]よりすべての自然数$n$について，$\sqrt{p}<a_{n}$が成り立つ．
3.の証明
$a_n-a_{n+1}>0$であることを示す．$$\begin{split}a_n-a_{n+1}&=a_n-\frac{1}{2}(a_{n}+\frac{p}{a_{n}})\\&=\frac{1}{2}a_n-\frac{p}{2a_n}\\&=\frac{1}{2}(a_n-\frac{p}{a_n})\\&=\frac{{a_n}^2-p}{2a_n}\end{split}$$ここで２．より$\sqrt{p}<a_{n}$であるから$2a_n>0$である．また，$\sqrt{p}<a_{n}$より，両辺は正の数だから２乗しても良いので$\sqrt{p}^2<a_{n}^2$となる．よって$p<a_{n}^2$となり$a_{n}^2-p>0$．したがって，$\frac{{a_n}^2-p}{2a_n}$$>0$となるので証明された．
性質から分かること
さて、以上の性質から得られることをまとめると、
１．より数列{$a_n$}はすべて有理数なので割り算をすれば具体的に値を求めることが可能である。
２．よりすべての$a_n$は$\sqrt{p}$より大きいことが分かり。
３．から数列{$a_n$}は$n$が大きくなるにつれて$a_n$が小さくなることが分かる。したがって結論は次の通りである。
$$\sqrt{p}<・・・<a_{n+1}<a_n<・・・<a_2<a_1=aが成り立つ$$
数列{$a_n$}を用いることでいくらでも$\sqrt{p}$に近い値を求めることができる．次では実際に$\sqrt{7}$の近似値を求めてみよう。
$\sqrt{7}$の近似値をニュートン・ラフソン法を用いて求める。
$\sqrt{4}<\sqrt{7}<\sqrt{9}$より，$2<\sqrt{7}<3$だから$a_1=3$とおく．
$$\begin{split}a_2&=\frac{1}{2}(a_{1}+\frac{7}{a_{1}})\\&=\frac{1}{2}(3+\frac{7}{3})\\&=\frac{8}{3}\\&\fallingdotseq2.666666666・・・\end{split}$$
このようにして，$a_3$，$a_4$と求めてみる．
$$\begin{split}a_3&=\frac{1}{2}(a_{2}+\frac{7}{a_{2}})\\&=\frac{1}{2}(\frac{8}{3}+\frac{7}{\frac{8}{3}})\\&=\frac{127}{48}\\&\fallingdotseq2.645833333・・・\end{split}$$
$$\begin{split}a_4&=\frac{1}{2}(a_{3}+\frac{7}{a_{3}})\\&=\frac{1}{2}(\frac{127}{48}+\frac{7}{\frac{127}{48}})\\&=\frac{32257}{12192}\\&\fallingdotseq2.645751312・・・\end{split}$$
このようにして考えると$\sqrt{7}\fallingdotseq2.645751312・・・$より少し小さい値かなとみることができる．
実際，$\sqrt{7}\fallingdotseq2.64575131106・・・$なので$a_4$を求めただけでもかなり良い近似を得られたと考えられるのではないか．
漸化式の導出方法
そもそもどのような考えに基づいて
$$a_{n+1}=\frac{1}{2}(a_{n}+\frac{p}{a_{n}})$$
という漸化式が導出されているかについて述べる。
求めたい平方根$\sqrt{p}$に対して，$f(x)=x^2-p$とおく．
$$y=f(x)$$
のグラフに対して$x$軸との交点のうち，$x$座標が正になっている方の$x$座標は$\sqrt{p}$である．
$a-1<\sqrt{q}<a$を満たす自然数を$a$とし，$a_1=a$とおく．
そして，$(a,f(a))$における$y=f(x)$の接線と$x$軸との交点の$x$座標を$a_2$とおく．
$(a_2,f(a_2))$における$y=f(x)$の接線と$x$軸との交点の$x$座標を$a_3$とおく．これを繰り返す．
つまり，$(a_n,f(a_n))$における$y=f(x)$の接線と$x$軸との交点の$x$座標を$a_{n+1}$とおく．
すると，$(a_n,f(a_n))$における接線の方程式は
$$y-f(a_n)=f'(a_n)(x-a_n)$$
接線の傾きは$f'(a_n)=2a_n$なので
$$y-({a_n}^2-p)=2a_n(x-a_n)$$
より$x$軸との交点の$x$座標は$y=0$を代入して
$$x=\frac{1}{2}(a_{n}+\frac{p}{a_{n}})$$
となるので，$$a_{n+1}=\frac{1}{2}(a_{n}+\frac{p}{a_{n}})$$が導かれる．
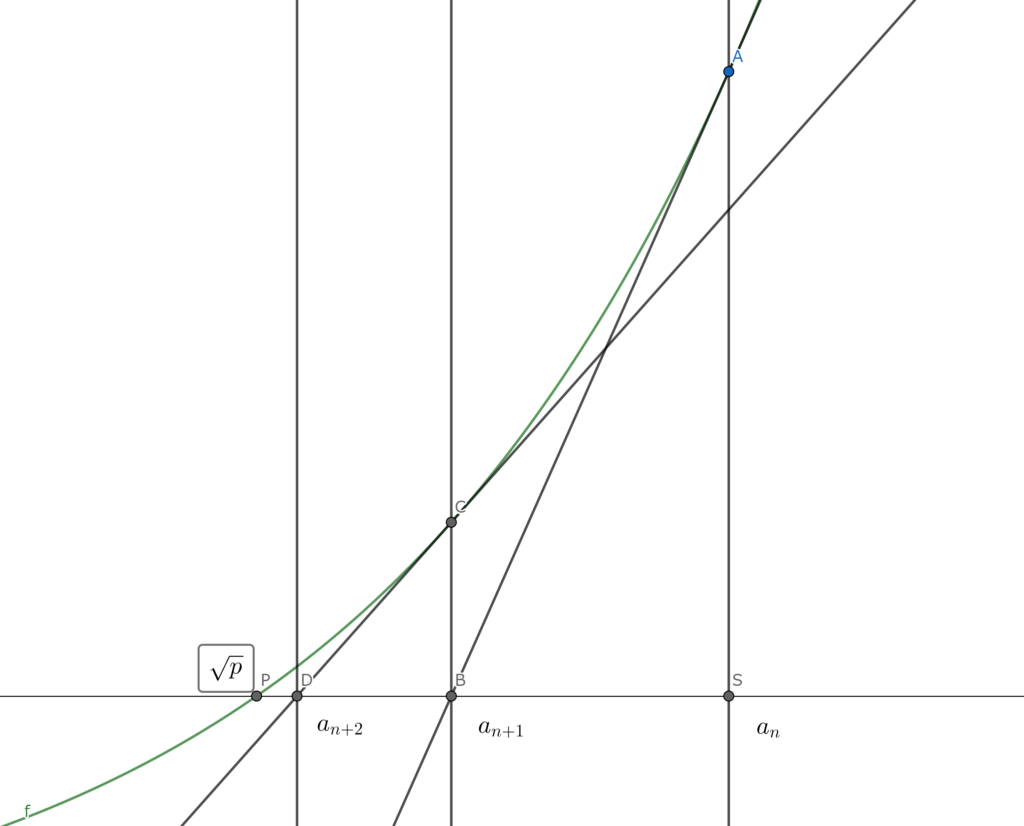
緑色のグラフが$y=x^2-p$であり，点Pの座標が$(\sqrt{p},0)$である．
グラフを見ると，数列$a_n$は単調減少し，かつ$\sqrt{p}$より小さくなるこはないことが視覚的にわかるであろう．
まとめ
今回はニュートン・ラフソン法による平方根の近似値の求め方について述べた．
もし今後，試験中なので平方根の近似値を求めなければいけないときはぜひ使ってみてほしい．
コメント