高校生が常用対数表を使う機会といえば、たいていの場合「桁数を求める問題」や
「小数第何位に初めて0以外の数が現れるか求める問題」がほとんどではないでしょうか。
そのため、「それ以外の用途で常用対数表を使うことはない」と
思い込んでいる人も多いはずです。
そこで今回は、そんな少し影の薄い常用対数表を使って、
桁数や小数首位の問題以外の「数値計算」 を解説していきます。
電卓のない時代、人々がどのように計算していたのか、その一端に触れてみましょう。
1. そもそも常用対数とは
常用対数とは、対数 ($\log$) の底が $10$ であるもののことです。
例えば $\log_{10}{5}$ や $\log_{10}{7}$ のようなものを指します。
これらの値はほとんどの場合「無理数(循環しない無限小数)」になるため、
計算しやすいように近似値を一覧にした常用対数表が教科書の巻末などに掲載されています。
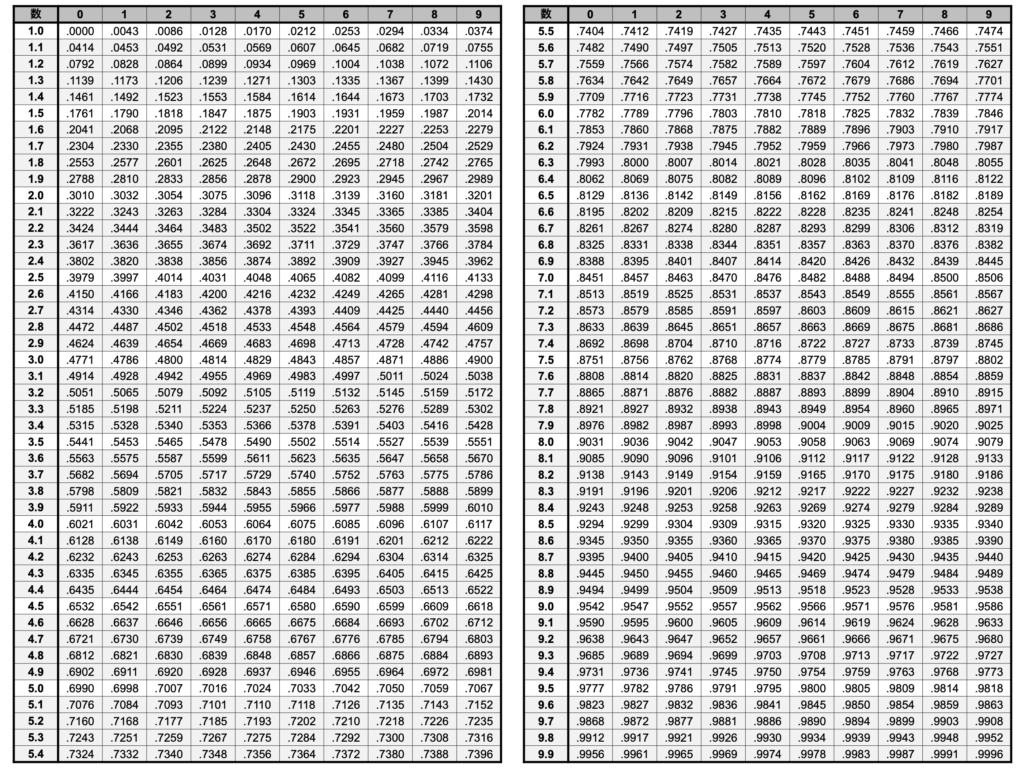
1-1. 復習:計算に使う対数の性質
今回の計算を行ううえで、以下の2つの性質が必要不可欠です。
軽く確認しておきましょう。
① $\log_{a}{M^k}=k\log_{a}{M}$
② $\log_{a}{MN}=\log_{a}{M}+\log_{a}{N}$
2.【実践】常用対数表で近似値を求める
では、実際に以下の値を常用対数表を用いて求めてみましょう。
例題:次のおおよその値を常用対数表を用いて求めなさい。
(1) $1.1^{40}$
(2) $12.3^{5}$
(3) $0.514^{10}$
どの値も、実際に筆算で40乗や10乗の計算をするのは現実的ではありません。
大学入試で直接問われる可能性は低いかもしれませんが、
対数の仕組みを深く理解するために、ぜひ手を動かして考えてみてください。
(1) $ 1.1^{40}$ の計算
まずは $1.1^{40}$ に常用対数をとって計算を進めます。
$$\begin{split} \log_{10}{1.1^{40}} &= 40\log_{10}{1.1} \quad (\text{性質①}) \\ &= 40 \times 0.0414 \quad (\text{常用対数表より}) \\ &= 1.656 \\ &= 1 + 0.656 \quad (\text{整数部分と小数部分に分ける}) \end{split}$$
ここで、式の形を $\log$ に戻していきます。
常用対数表を逆引き(表の中から0.656に近い値を探す)すると、$\log_{10}{4.53} \fallingdotseq 0.656$ であることがわかります。
$$\begin{split} (\text{続き}) \quad &= \log_{10}{10} + \log_{10}{4.53} \\ &= \log_{10}{(10 \times 4.53)} \quad (\text{性質②}) \\ &= \log_{10}{45.3} \end{split}$$
元の数が $\log_{10}{45.3}$ と等しいことがわかったので、答えは以下のようになります。
解答:
$$1.1^{40} \fallingdotseq 45.3$$
(2) $ 12.3^{5}$ の計算
常用対数表には、真数が $1.00 \sim 9.99$ の値しか載っていません。
そのため、$12.3$ のような数は、$1.23 \times 10$ のように
「1以上10未満の数 × 10の累乗」の形に変形してから対数をとるのがコツです。
$$\begin{split} \log_{10}{12.3^{5}} &= 5\log_{10}{12.3} \\ &= 5\log_{10}{(10 \times 1.23)} \\ &= 5(\log_{10}{10} + \log_{10}{1.23}) \quad (\text{性質②}) \\ &= 5(1 + 0.0899) \quad (\text{常用対数表より}) \\ &= 5 \times 1.0899 \\ &= 5.4495 \\ &= 5 + 0.4495 \end{split}$$
ここで表を逆引きします。$0.4495$ に近い値を探すと、$2.82$ 付近であることがわかります($\log_{10}{2.82} \approx 0.4502$)。
$$\begin{split} (\text{続き}) \quad &= \log_{10}{10^5} + \log_{10}{2.82} \\ &= \log_{10}{(10^5 \times 2.82)} \\ &= \log_{10}{282000} \end{split}$$
解答:
$$12.3^{5} \fallingdotseq 282000$$
(3) $ 0.514^{10}$ の計算
(2)と同様に、真数部分を調整してから計算します。
特に計算結果が負の数になる場合は、最後の変形で注意が必要です。
$$\begin{split} \log_{10}{0.514^{10}} &= 10\log_{10}{0.514} \\ &= 10\log_{10}{(10^{-1} \times 5.14)} \\ &= 10(\log_{10}{10^{-1}} + \log_{10}{5.14}) \\ &= 10(-1 + 0.7110) \quad (\text{常用対数表より}) \\ &= 10 \times (-0.289) \\ &= -2.89 \end{split}$$
ここで、$-2.89$ を整数部分と小数部分に分けます。
常用対数表の値はすべて「正の数」なので、小数部分は必ずプラスにしなければなりません。
$$\begin{split} (\text{続き}) \quad &= -3 + 0.11 \quad (\text{※ -2-0.89 ではないことに注意!}) \\ &= \log_{10}{10^{-3}} + \log_{10}{1.29} \quad (\text{表より逆引き}) \\ &= \log_{10}{(10^{-3} \times 1.29)} \\ &= \log_{10}{0.00129} \end{split}$$
解答:
$$0.514^{10} \fallingdotseq 0.00129$$
3. 計算の重要ポイント

これらの計算において最もつまずきやすいポイントは、
(3)で扱ったような「計算結果が負の数になったときの処理」です。
例えば $-2.89$ が出てきたとき、
- $\times \quad -2 – 0.89$ (小数部分がマイナスになってしまい、表が使えない)
- $\bigcirc \quad -3 + 0.11$ (あえて引いてから足すことで、小数部分をプラスにする)
このように小数部分を正の数にするという操作を忘れなければ、
自由に値を復元することができます。
ここさえしっかり押さえておけば難しくありません。
4. まとめ
対数の数値計算は、今の大学入試ではあまり重要視されていないテクニックかもしれません。
しかし、フランスの数学者ラプラスが残した「対数は天文学者の寿命を2倍にした」という言葉があるように、対数は歴史上、計算革命のツールとして絶大な威力を発揮しました。
かつては巨大な数の掛け算を何日もかけて筆算していたものが、対数表を使うことで、簡単な足し算に置き換わり、計算時間が劇的に短縮されたのです。
「桁数」や「最高位」を求めるだけでなく、たまには先人たちに思いを馳せて、近似値計算の素晴らしさを味わってみてください。




コメント