第1章:数学の基本定数、$\pi$ の謎に迫る!
皆さん、円周率 $\pi$(パイ)が約 $3.14159\dots$ であることは知っていますね。円の面積や周の長さを計算するときに必ず登場する、数学の世界で最も重要な定数の一つです。
しかし、もし私が「針を床に投げるだけで、$\pi$ のおおよその値を求めることができる」と言ったら、信じられますか?
「円周率なのに、円も使わずにどうやって?」
そう思いますよね。この一見不可能な挑戦を可能にするのが、今から約 250 年前のフランスの数学者、ジョルジュ=ルイ・ルクレール・ド・ビュフォンによって考案された、「ビュフォンの針」という驚くべき実験です。
🧵 準備:シンプルな実験設定
必要なものは、非常にシンプルです。
1. 床に等間隔の平行線を引く
・線の間隔は、後で解説しますが、針の長さと関連づけておきます。
例えば、間隔を $L$ としましょう。

2. 短い針をたくさん用意する
・針の長さは、線の間隔 $L$ 以下にしておきます(同じ長さでもOK)。
針の長さを $l$ としましょう。

この状態で、針を床の上にランダムに投げ入れます。
❓ 問いかけ:偶然の中に潜む必然
想像してみてください。何百本、何千本と針を投げたとき、その針の何本が「平行線と交差したか」を数えます。
全投下本数と交差した本数。このたった二つの数字の比率を計算するだけで、なんと数学の神秘的な定数である円周率 $\pi$ が姿を現すのです。
交差した針を赤で表示しています。
どうして、ランダムな針の動きが、円の性質を示す定数 $\pi$ と結びつくのでしょうか?そして、そこにはどのような数学的な法則が隠されているのでしょうか?
次章では、この驚きの現象の裏側にある、「確率」と「解析学」の美しい関係について、詳しく解説していきます!
第2章:確率の計算に潜む $\pi$ の正体
前章では、針を投げるというランダムな実験で円周率 $\pi$ が求まるという不思議な現象を紹介しました。この謎を解く鍵は、「針の位置」と「針の角度」という二つの要素が関係する確率の計算にあります。
この実験では、次の条件を設定します。
- 平行線の間隔:$L$
- 針の長さ:$l$ (ただし、$l \leqq L$)
針の「位置」と「角度」を考える
一本の針が線と交差するかどうかは、針がどこに落ち、どの向きを向いたかで決まります。この二つの要素を数学的に表現しましょう。
① 針の「位置」:線からの距離 $d$
針の中心から、最も近い平行線までの垂直距離を $d$ とします。
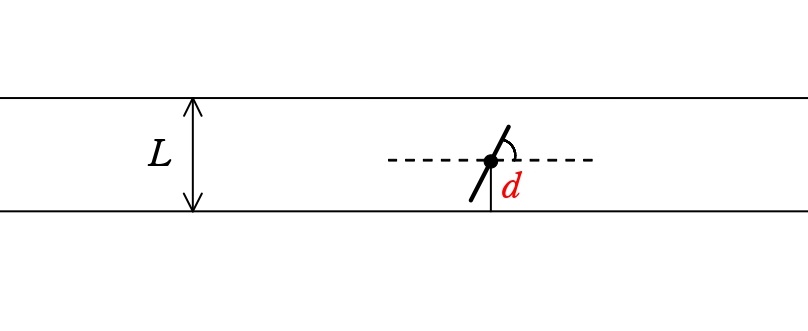
- $d$ は $0$ から $\frac{L}{2}$ の間でランダムに決まります。
そして同様に確からしくなります。
② 針の「角度」:水平線とのなす角 $\theta$
針が水平線(平行線と垂直な方向)に対してなす角を $\theta$(シータ)とします。
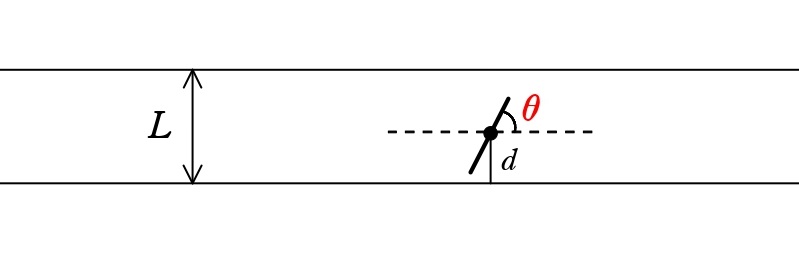
- $\theta$ は $0^\circ$ から $180^\circ$(または $0$ から $\pi$ ラジアン)の間でランダムに決まります。
そしてこちらも、同様に確からしくなります。
交差する条件を三角関数で表す
針が線と交差するのは、針の先端が線まで届いたときです。
針を垂直な方向(線と線をつなぐ方向)に投影したときの長さを考えてみましょう。この長さは、針の長さ $l$ と角度 $\theta$ を使って、$l \sin\theta$ で表されます。(三角関数、覚えていますか?)
針の中心から線までの距離 $d$ が、この投影された長さの半分 $\frac{l \sin\theta}{2}$ よりも短ければ、針は線と交差します。
注意:下の図は交差しない場合の図です。
$$\text{交差しない条件:} \quad d > \frac{l \sin\theta}{2}$$
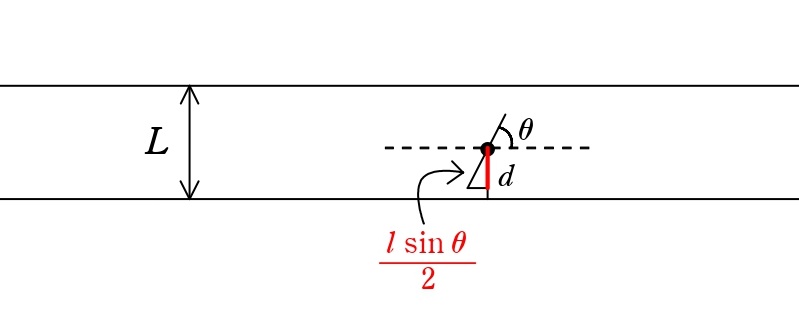
したがって,交差する条件は以下のようになる。
$$\text{交差する条件:} \quad d \leqq \frac{l \sin\theta}{2}$$
確率の領域(幾何学的確率)
高校数学の「確率」の分野で、面積や長さを利用して確率を求める幾何学的確率を少し応用して考えます。
針の位置 $d$ と角度 $\theta$ を座標としてグラフで表すと、起こり得るすべてのパターンは一つの大きな長方形の領域になります。
$\propto$は比例記号
$y$ が $x$ に比例するときは $y \propto x$ と書く。
- 全事象の領域(全てのパターン): $d$ が $0$ から $\frac{L}{2}$、$\theta$ が $0$ から $\pi$ の範囲。
- 領域の面積 $\propto$ 全投下本数
- 交差する事象の領域(交差するパターン): $d \le$ $\frac{l \sin\theta}{2}$ を満たす部分。
- 領域の面積 $\propto$ 交差した本数
$$\text{交差する確率 } P = \frac{\text{交差する領域の面積}}{\text{全事象の領域の面積}}$$
解析学の力!積分の出番
高校3年生で学ぶ「積分」(解析学の重要なツール)を使うと、この交差する領域の面積を求めることができます。
① 全事象の領域の面積(全てのパターン)
針の中心から線までの距離 $d$ の範囲は $0 \le d \le \frac{L}{2}$、針の角度 $\theta$ の範囲は $0 \le \theta \le \pi$(ラジアン)です。
この領域は、縦が $\frac{L}{2}$、横が $\pi$ の長方形になります。
$$\text{全事象の領域の面積} = (\text{縦}) \times (\text{横})$$
$$\text{全事象の領域の面積} = \frac{L}{2} \times \pi = \frac{\pi L}{2}$$
② 交差する事象の領域の面積(交差するパターン)
針が線と交差する条件は $d \leqq$ $\frac{l \sin\theta}{2}$ でした。この領域の面積は、関数 $y =$ $\frac{l \sin\theta}{2}$ のグラフと $\theta$ 軸で囲まれた部分の面積を求めることで得られます。これが積分の考え方です。
$$\text{交差する領域の面積} = \int_{0}^{\pi} \frac{l \sin\theta}{2} d\theta$$
ここで、積分計算の途中の式を見てみましょう。定数である $\frac{l}{2}$ を積分の外に出します。
$$= \frac{l}{2} \int_{0}^{\pi} \sin\theta d\theta$$
$\sin\theta$ の不定積分は $-\cos\theta$ なので、これに $\pi$ と $0$ を代入します。
$$= \frac{l}{2} \left[ -\cos\theta \right]_{0}^{\pi}$$
$$= \frac{l}{2} \left( (-\cos\pi) – (-\cos 0) \right)$$
ここで、$\cos\pi = -1$、$\cos 0 = 1$ を代入します。
$$= \frac{l}{2} \left( (-(-1)) – (-1) \right)$$
$$= \frac{l}{2} \left( 1 – (-1) \right)$$
$$= \frac{l}{2} \times 2 = l$$
したがって、交差する領域の面積は $l$ となります。
確率 $P$ の計算
確率 $P$ は、交差する領域の面積を全事象の領域の面積で割ることで求められます。
$$\text{交差する確率 } P = \frac{\text{交差する領域の面積}}{\text{全事象の領域の面積}}$$
$$P = \frac{l}{\frac{\pi L}{2}}$$
分母の分数を整理すると、見覚えのある形が現れます。
$$P = \frac{2l}{\pi L}$$
🌟 結論:$\pi$ が姿を現す!
この理論的な確率 $P =$ $\frac{2l}{\pi L}$ は、実際に針を投げたときの確率 $\frac{\text{交差した本数}}{\text{全投下本数}}$ と等しくなるはずです。
$$P_{\text{実験}} \approx P_{\text{理論}} \quad \Rightarrow \quad \frac{\text{交差した本数}}{\text{全投下本数}} \approx \frac{2l}{\pi L}$$
この式を $\pi$ について解き直せば…
$$\pi \approx \frac{2l}{L} \times \frac{\text{全投下本数}}{\text{交差した本数}}$$
このように、針の長さ $l$ と間隔 $L$、そして実験結果である本数の比率という、円とは全く関係ない要素から、円周率 $\pi$ を近似的に求めることができるのです!
第3章:実際に $\pi$ を求めてみよう!🚀【実験と考察】
実験の準備とルール設定
ビュフォンの針の実験は、特別な装置は一切不要です。家にあるシンプルな道具で、数学の神秘に触れてみましょう!
必要なもの
- 床または広い紙: 等間隔の線を引くための場所。
- 定規とペン: 平行線を正確に引くために使います。
- 針の代わりになるもの (長さ $l$)
例: 爪楊枝、クリップ、短く切ったストローなど。 - 記録用紙: 投下回数と交差回数を記録します。
✨ 実験の簡略化テクニック:$l = L$ の設定
前章で導いた公式はこれでしたね。
$$\pi \approx \frac{2l}{L} \times \frac{\text{全投下本数}}{\text{交差した本数}}$$
ここで、もし「針の長さ $l$」と「平行線の間隔 $L$」をまったく同じ長さに設定すれば、式が劇的に簡単になります!
$$\pi \approx \frac{2 \times L}{L} \times \frac{\text{全投下本数}}{\text{交差した本数}}$$
$$\pi \approx 2 \times \frac{\text{全投下本数}}{\text{交差した本数}}$$
このシンプルな式を使うために、
$l$ と $L$ を同じ長さ(例:5cm)に設定することをおすすめします。
実験の手順(最低100回チャレンジ!)
より正確な $\pi$ の値を得るためには、「たくさんの回数」投げることが重要です。まずは最低100回を目標にやってみましょう。
結果の計算と考察
さあ、いよいよ集計したデータを使って、円周率 $\pi$ の値を計算してみましょう!
$$\pi \approx 2 \times \frac{N}{C}$$
【例】 あなたが100回針を投げて、64回線と交差したとします。
$$\pi \approx 2 \times \frac{100}{64} = 2 \times 1.5625 = 3.125$$
本来の $\pi \approx 3.14159\dots$ にかなり近い値が出ましたね!
📈 考察のポイント:なぜズレるのか?
なぜ、あなたの実験結果は本当の $\pi$ の値から少しズレてしまうのでしょうか?
それは、「大数の法則」が関係しています。
- 大数の法則: 確率的な事象は、試行回数を増やせば増やすほど、その結果が理論上の確率に近づいていくという法則です。
- 考察: あなたが投げる回数 $N$ が少なければ少ないほど、偶然に左右され、計算された $\pi$ の値は大きくバラつきます。逆に、1,000回、10,000回と試行を増やしていけば、あなたの計算した $\pi$ の値は、数学的な真実である $3.14159\dots$ に限りなく近づいていくのです。
ランダムな現象の中に、数学の真理が隠されている。これこそが、このビュフォンの針が示す、確率と解析学の美しい結びつきなのです。
🌟 まとめ:確率の力で数学定数を支配する
ビュフォンの針は、「円」とは全く関係のない「直線」と「偶然」の組み合わせから、
円周率 $\pi$ という円の定数を導き出すという、驚きに満ちた実験です。
この実験は、高校で学ぶ確率や三角関数といった知識が、一見ランダムに見える世界を解析する解析学と深く結びついていることを教えてくれます。
この世界は、あなたの知っている数学の知識で解き明かせる法則に満ちているのです。




コメント