皆さん、「美しい」と感じるデザインや比率には、実は共通の数学的な秘密が隠されているとしたら、どう思いますか?
私たちが「完璧だ」と感じる古代ギリシャの神殿、ルネサンスの名画、そして私たちの体…。これらすべてを支配している、たった一つの魔法の数字があるのです。それが、今日探求するテーマ「黄金比($\phi$ファイ)」です。
1. 黄金比$\phi$とは
黄金比は、およそ 1:1.618 の比率を持つ数字です。
この比率は、ただの数字ではありません。古代の数学者が「最も調和のとれた比率」として発見して以来、何世紀にもわたって建築や芸術に取り入れられてきました。
- ルネサンスの巨匠たちは、キャンバスに描かれる人体の比率に$\phi$を取り入れました。
- アップルのロゴなどの現代のデザインにも、その美しさが応用されていると言われます。
1-1. 自然界の「デザインコード」
しかし、$\phi$の真に驚くべき力は、自然界の中にあります。
ひまわりの種の並び方、松ぼっくりのうろこ、さらには私たちが毎日目にしている木の枝分かれ方や川の流れのパターンまで、この比率が関わっているのです。
なぜ自然は、わざわざこの$\phi$という数字を選んでいるのでしょうか?
1-2. 「完璧な美しさ」の裏にある数学
本記事では、この黄金比 $\phi$ が何であるかを定義するところから始め、高校で習う数列や二次方程式を使ってその正体に迫ります。
さらに、$\phi$が持つ「自己相似性」という特殊な性質が、フラクタルという無限に複雑な幾何学的なパターンを生み出し、自然界のあらゆる場所に美と秩序を与えている理由を深掘りしていきます。
身の回りの世界が、実は数学のルールでデザインされていたという驚きの発見を、一緒に体験しましょう!
2. 黄金比 $\phi$ の正体:代数と幾何から考える

代数(Algebra): 文字($x$,$y$ など)を使って数や量の関係を表し、方程式などを使って未知の値を求める数学の分野です。
幾何(Geometry): 図形(三角形、円など)の形や大きさ、位置関係を調べ、面積や角度を計算する数学の分野です。
これらを用いて黄金比$\phi$を考えていきます。
2-1. 幾何学的な定義:最も美しい「分け方」
「黄金比」は、ただ美しいとされるだけでなく、厳密な数学的定義を持っています。
ある一本の線分があると想像してください。この線分を途中の点で二つの部分(長い部分 $a$ と短い部分 $b$)に分けるとき、次の比率の「等式」が成り立つようにします。
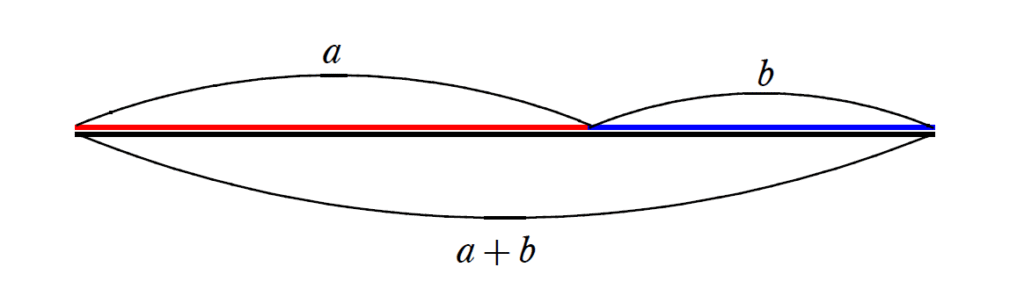
全体:長い部分=長い部分:短い部分
これを $a$ と $b$ を使って式で表すと、次のようになります。
$$\begin{eqnarray}
(a+b):a &=& a:b \\
\frac{a}{b} &=& \frac{a+b}{a}
\end{eqnarray}$$
この比率 $(=\frac{a}{b})$ の値こそが、黄金比 $\phi$ $(=\frac{a}{b})$ の正体です。つまり、黄金比とは、「最も調和がとれた自己言及的な比率」として定義されるのです。
2-2. 二次方程式で $\phi$ を計算する
では、この比率 $\phi$ は一体いくつの値になるのでしょうか? 高校で習う二次方程式を使って、$\phi$ の厳密な値を計算してみましょう。
$$\phi = \frac{a}{b}$$
まず、定義式 $\frac{a}{b} = \frac{a+b}{a}$ を変形します。
- 分数を分解する: 右辺の分数を分解します。
$$\frac{a}{b} = 1 + \frac{b}{a}$$ - $\phi$ に置き換える: ここで $\frac{a}{b}$$=\phi$ であり、$\frac{b}{a}$ はその逆数 $\frac{1}{\phi}$ なので、式を $\phi$ だけで表すことができます。
$$1 + \frac{1}{\phi} = \phi$$ - 二次方程式に整理する: 分母を払うために両辺に $\phi$ をかけると、二次方程式が現れます。
$$\phi^2 – \phi – 1 = 0 \quad (\phi > 0)$$
2-3. $\phi$ の厳密な値の導出
この二次方程式を、皆さんが知っている解の公式で解いてみましょう。
$$\begin{eqnarray}
\phi &=& \frac{-(-1) \pm \sqrt{(-1)^2 – 4・1・(-1)}}{2・1} \\
&=& \frac{1 \pm \sqrt{5}}{2}
\end{eqnarray}$$
$\phi$ は比率であり、線分の長さから定義されているため、必ず正の値 ($\phi$>0) を取ります。したがって、マイナスの解は不適であり、黄金比 $\phi$ の厳密な値は、
$$\phi = \frac{1 + \sqrt{5}}{2}$$
となります。
電卓で計算すると、
$$\phi \approx 1.6180339887…$$
となり、円周率$\pi$ や 自然対数の底$e$ と同じく、この黄金比 $\phi$ は永遠に続く無理数であることがわかります。これが、最も美しいとされる比率の「数学的なパスポート」です。
2-4. 次の展開へ
これで、黄金比 $\phi$ の定義と値を理解しました。しかし、この$\phi$ が、なぜ私たちの身の回りの自然界に頻繁に現れるのでしょうか? 次のセクションでは、$\phi$ が成長のルールから自然に生まれる数字であることを、フィボナッチ数列を使って見ていきましょう。
3. フィボナッチ数列と $\phi$ との関係
3-1. 成長のルール:フィボナッチ数列の紹介 🐇
前のセクションで、黄金比 $\phi$ が代数的に $\boldsymbol{\frac{1+\sqrt{5}}{2}}$ と定義されることを知りました。しかし、この数字が自然界のどこからやってくるのでしょうか?その答えは、「成長のルール」を表現するフィボナッチ数列にあります。
フィボナッチ数列 $\boldsymbol{\{F_n\}}$ は、以下のシンプルなルールで定義されます。
$$\text{次の数} = \text{前の数} + \text{その前の数}$$
つまり、最初の $2$ 項を $1$ とすると、
$$F_n = F_{n-1} + F_{n-2}$$
となります。具体的に書き出すと、以下の数列が得られます。
$$1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, \dots$$
この数列は、ウサギの増殖や植物の枝分かれなど、自然界の成長パターンをモデル化するために発見されました。
3-2. 黄金比 $\phi$ の再登場:比率の計算
このフィボナッチ数列の項を大きくしていくと、ある驚くべき現象が起こります。
それは、隣り合う項の比 $\boldsymbol{\frac{F_{n+1}}{F_n}}$ を計算し続けると、その値が黄金比 $\phi$ に収束していくということです。
数列の比率をいくつか計算してみましょう。
- $\frac{3}{2}$ $= 1.5$
- $\frac{5}{3}$ $\approx 1.6667$
- $\frac{8}{5}$ $= 1.6$
- $\frac{13}{8}$ $= 1.625$
- $\frac{21}{13}$ $\approx 1.6154$
- $\frac{34}{21}$ $\approx 1.6190$
計算を進めるごとに、比率は $1.61803…$ という$\phi$の値にどんどん近づいていくことが分かります。
3-3. $\phi$ への「収束」が意味するもの
高校で学ぶ数列の極限の言葉を使えば、この関係は次のように表現できます。
$$\lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi = \frac{1 + \sqrt{5}}{2}$$
これは、フィボナッチ数列の成長の比率が、最終的に黄金比 $\phi$ で安定することを意味しています。
- 直感的な解釈: $\phi$ は、自己増殖や成長を繰り返すシステムが最も安定して効率的に成長するための「究極の比率」であると解釈できます。
前のセクションで代数的に定義された $\phi$ が、ここでは自然の成長ルールの中から「自動的」に現れました。
3-4. 次の展開へ
この「究極の成長の比率」である $\phi$ が、なぜひまわりの種や貝殻の形にまで現れるのでしょうか?次のセクションでは、$\phi$ が持つ幾何学的な安定性、黄金螺旋の秘密に迫り、その謎を解き明かします。
4. 自然の秘密:黄金螺旋と配置の最適化
4-1. 永遠に続く図形:黄金長方形と自己相似 📐
前のセクションで、黄金比 $\phi$ が成長の安定した比率であることを知りました。ここでは、$\phi$ が持つ幾何学的な安定性を見ていきましょう。
辺の比が黄金比 $\phi$ である長方形を黄金長方形と呼びます。この図形には、驚くべき性質があります。
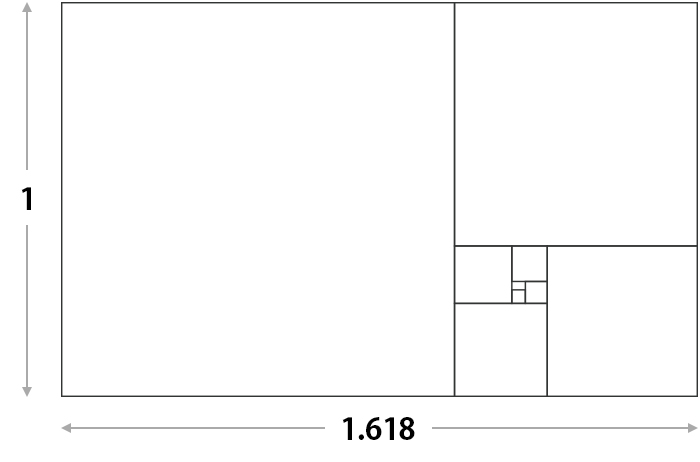
- 正方形を切り取る: 黄金長方形から、長い辺を $a$、短い辺を $b$ としたとき、$b \times b$ の正方形を切り取ります。
- 残った図形: 切り取った後に残る長方形(残りの部分)の辺の比は、$\phi$ の定義より $\boldsymbol{b : (a-b)}$ となります。
- 再び $\phi$: 実はこの残った長方形も、再び黄金長方形になっています。
このプロセスは無限に繰り返すことができます。全体の一部が、全体と全く同じ形(相似)をしているこの性質を自己相似性 (Self-Similarity) と呼びます。これが、記事のテーマの一つであるフラクタルの基本原理です。
4-2. 成長の軌跡:美しい黄金螺旋

この永遠に続く黄金長方形の分割を利用して、**黄金螺旋(対数螺旋)**を描くことができます。
- 分割した正方形の中に、円弧(四分円)を順番に描いていきます。
- この円弧をつなげていくと、渦巻状の美しい曲線が描かれます。これが黄金螺旋です。
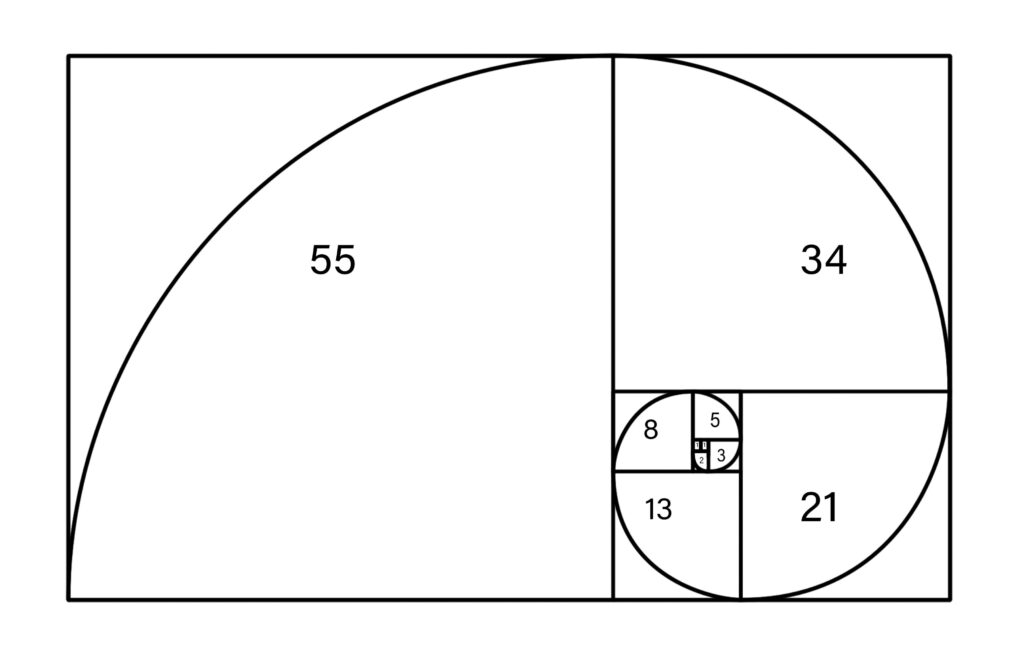
この黄金螺旋は、成長するにつれて形が変わらない(相似性を保つ)という特性を持っています。この特性こそが、自然界で効率の良い成長や空間の埋め方に使われているカギなのです。
4-3. ひまわりの謎:最適な配置角度 🌻
黄金螺旋は、巻貝(オウムガイなど)の殻や、宇宙の銀河の渦巻き構造など、非常に広いスケールで見られます。中でも、植物の種の配置に見られる現象は驚きです。

- ひまわりの種: ひまわりの花の中の種は、時計回りと反時計回りの $2$ 種類の螺旋を描いて密に詰まっています。
- 黄金角: この種の配置は、一つ前の種から約 $\mathbf{137.5^\circ}$ ずれた角度で次の種を配置することで実現されます。この $\mathbf{137.5^\circ}$ は黄金角と呼ばれ、円を黄金比で分けた角度に相当します。
$$\text{黄金角} = 360^\circ \times \left(1 – \frac{1}{\phi}\right) \approx 137.508^\circ$$
なぜこの角度が最適なのか?
もしこの角度がシンプルな分数(例:$120^\circ = 360^\circ / 3$)であれば、種は放射状の直線上に並んでしまい、中心付近に大きな隙間ができてしまいます。
しかし、黄金角 ($\phi$) は最も無理数らしい無理数であるため、この角度で次の種を配置すると、絶対に同じ場所に重なることなく、最も均等に、最も効率よく空間を埋めることができるのです。
つまり、黄金比 $\phi$ は、自然が空間を最大限に活用し、最も効率よく設計するために選んだ「デザインコード」なのです。
5. まとめ
黄金比 $\phi$ は、単なる美しい比率ではありません。
- 代数的定義 ($\phi^2 – \phi – 1 = 0$) に基づき、
- フィボナッチ数列の成長のルールから導かれ、
- 自己相似性を通じて、自然界の配置の最適化を可能にする、数学の必然が詰まった数字なのです。
数学の美しさは、私たちが住む世界の至る所に、秩序と効率という形で深く根付いているのですね!




コメント