【循環論法？】sinx/xのｘを0に近づけたときの極限の闇に迫る

はじめに

しばし話題になる$$\lim_{x\rightarrow0}\frac{\sin x}{x}=1$$の証明が高校数学では循環論法になってしまう問題．
確かに，数学Ⅲの教科書では扇形の面積を用いて証明を行っている．

循環論法になる問題点

ここで注目しなければならないのは扇形の面積は円の面積から求められる．
しかし，円の面積の公式は小学校で学ぶが証明はされていない．

なぜ円の面積は$r^2\pi$なのかは積分(三角関数を含む)を学ぶことによってきちんと証明される．
したがって，次のような問題が起こる．

循環論法になる部分

教科書では以下の図で

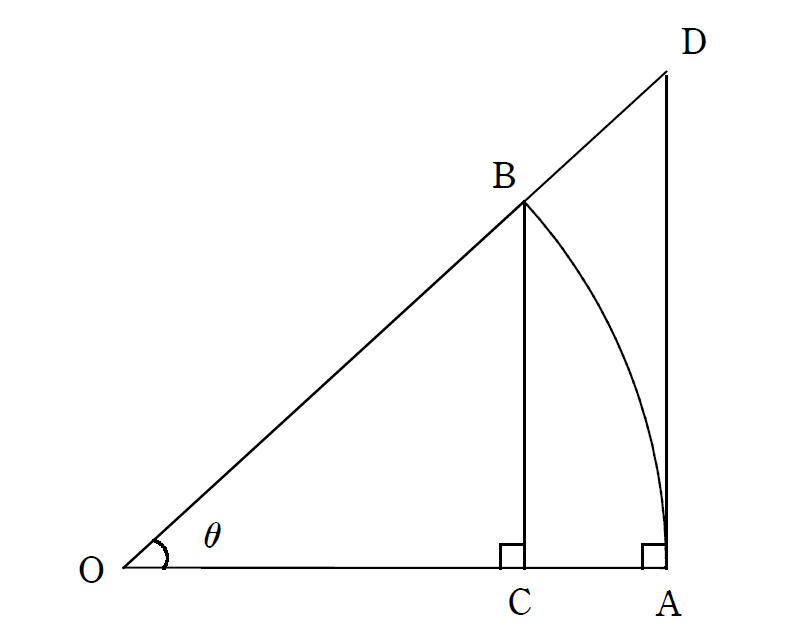
$\triangle$OBC　＜　扇形OAB　＜　$\triangle$ODA　から「はさみうちの原理」を用いている．

扇形の面積を用いる，ために

↓

積分をして円の面積を求める，ために

↓

その積分では三角積分をする，ために

↓

三角関数の微分をする，ために

↓
$$\lim_{x\rightarrow0}\frac{\sin x}{x}=1を用いる，ために$$
↓

扇形の面積を用いる，ために

↓
以下最初からループする．

このような循環論法を回避する証明をしていく．

循環論法を回避するアイディア

上の方法では円の面積を用いるので証明できなかった．

弧の長さを用いて証明をしていく．弧の長さならば公式等の制約を受けない．
円周と直径の関係については（円周）＝（直径）× $\pi$ と定義されているので心配無用．

循環論法を回避した証明

次の不等式を証明する．

AC < 弧AB ≦AC + CB

AC < 弧AB については明らか．よって弧AB <≦AC + CB を示す．
図を見れば明らかであるとしても良い気もするが，ここではきちんと証明する．

ここで次の定理を用いる．

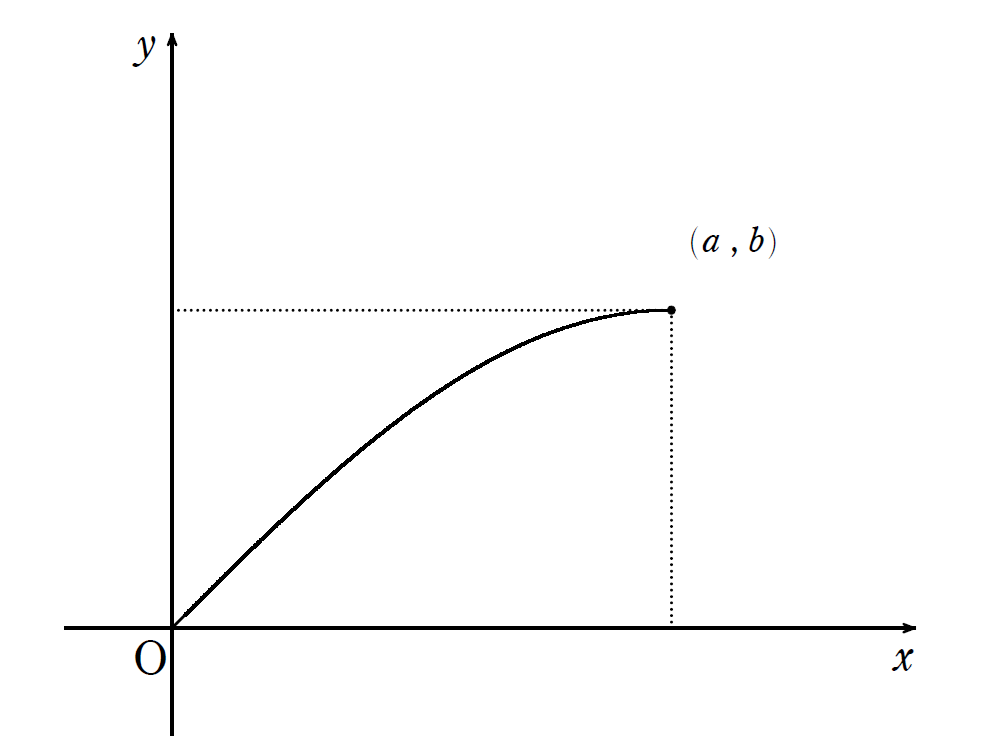
上の定理は言い換えると，
一方向にしか進まない曲線の長さは始点と終点を横に進んだ長さと縦に進んだ長さの和より短いというものである．つまり，この定理を証明できれば弧AB < AC + CB を示すことができるのだ．

証明

曲線を媒介変数$t$を用いて$x=f(t) , y=g(t)　(0\leqq t \leqq 1)$とする．
この$f(t),g(t)$は$0<t<1$に対して$f'(t)\geqq 0 , g'(t)\geqq 0$を満たし，
$f(0)=0 , f(1)=a , g(0)=0 , g(1)=b$とする．

曲線の長さ$L$は
$$\begin{eqnarray}
L &=& \int_{0}^{1}\sqrt{{f'(t)}^2+{g'(t)}^2}dt 　　　f'(t)\geqq 0 , g'(t)\geqq 0より　\\
&\leqq& \int_{0}^{1}\sqrt{{f'(t)}^2+2f'(t)g'(t)+{g'(t)}^2}dt \\
&=& \int_{0}^{1}\sqrt{(f'(t)+g'(t))^2}dt \\
&=& \int_{0}^{1}|f'(t)+g'(t)|dt 　　　　f'(t)\geqq 0 , g'(t)\geqq 0より　\\
&=& \int_{0}^{1}(f'(t)+g'(t))dt \\
&=& f(1)-f(0)+g(1)-g(0) \\
&=& a+b \\
\end{eqnarray}$$

よって証明ができる．

したがって，AからBまでの曲線（$x$軸方向と$y$軸方向で向きが変わらない）は$a+b$以下になるので
AC < 弧AB ≦AC + CBが示された．

上の図において半径1の円で，Aの座標を$(1,0)$，Bの座標を$(\cos\theta,\sin\theta)$とすると，
AC$=1-\cos\theta$，弧AB$=\theta$，BC$=\sin\theta$となるので，
AC < 弧AB ≦AC + CBに代入すると，

$\theta\longrightarrow+0$のときを考える。
$$\begin{eqnarray}
\sin\theta &< \theta \leqq& 1-\cos\theta+\sin\theta 　　　0<\theta<\frac{\pi}{2}より0<\cos\theta<1なので\\
\sin\theta &< \theta \leqq& 1-\cos^{2}\theta+\sin\theta \\
\sin\theta &< \theta \leqq& \sin^{2}\theta+\sin\theta 　　　\sin\theta\neq0なので\sin\thetaで割る\\
1 &< \frac{\theta}{\sin\theta} \leqq& \sin\theta+1 \\
\end{eqnarray}$$

ここで$\theta\longrightarrow+0$とするとはさみうちの原理により
$$1 < \frac{\theta}{\sin\theta} \leqq 1 \\$$
なので$$\lim_{\theta \to +0}\frac{\theta}{\sin\theta}=1$$
となる．

$\theta\longrightarrow-0$のときも同様にして
$$\lim_{\theta \to -0}\frac{\theta}{\sin\theta}=1$$
だから，
$$\lim_{\theta \to 0}\frac{\theta}{\sin\theta}=1$$が示される．
よって，逆数をとって，$\theta$を$x$にして
$$\lim_{x\rightarrow0}\frac{\sin x}{x}=1$$が示された．

おわりに

いかがでしたでしょうか。
円の面積は小学校で習うのだが証明は数学Ⅲを学ばないときちんと示すことができないのだ。
教科書ではなぜこの書き方で証明をしているのかはわからないが，ひとまず循環論法にはならないことを書き添えておく。

よい数学ライフを！